Existenz von Parallelen (SoSe 12): Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(→‎Beweis der Existenz von Parallelen)
(→‎Beweis der Existenz von Parallelen)
 
Zeile 13: Zeile 13:
  
  
−
Lösungsversuch Nummero6/Tchu Tcha Tcha:<br />
+
Lösungsversuch Nummero6/Tchu Tcha Tcha:<br />[[Datei:Parallel S1.png]]<br />[[Datei:Parallel S2.png]]<br />
−
Skizze folgt..<br />
+
 
 
(1) Nach der Ex. & Eind. des Lots gibt es eine Gerade durch P, welche senkrecht zu g ist.<br />
 
(1) Nach der Ex. & Eind. des Lots gibt es eine Gerade durch P, welche senkrecht zu g ist.<br />
 
(2) <math>\left| l \right| = \left| \overline{SP}  \right|</math> // Vor., (1), Abstandsaxiom<br />
 
(2) <math>\left| l \right| = \left| \overline{SP}  \right|</math> // Vor., (1), Abstandsaxiom<br />
 
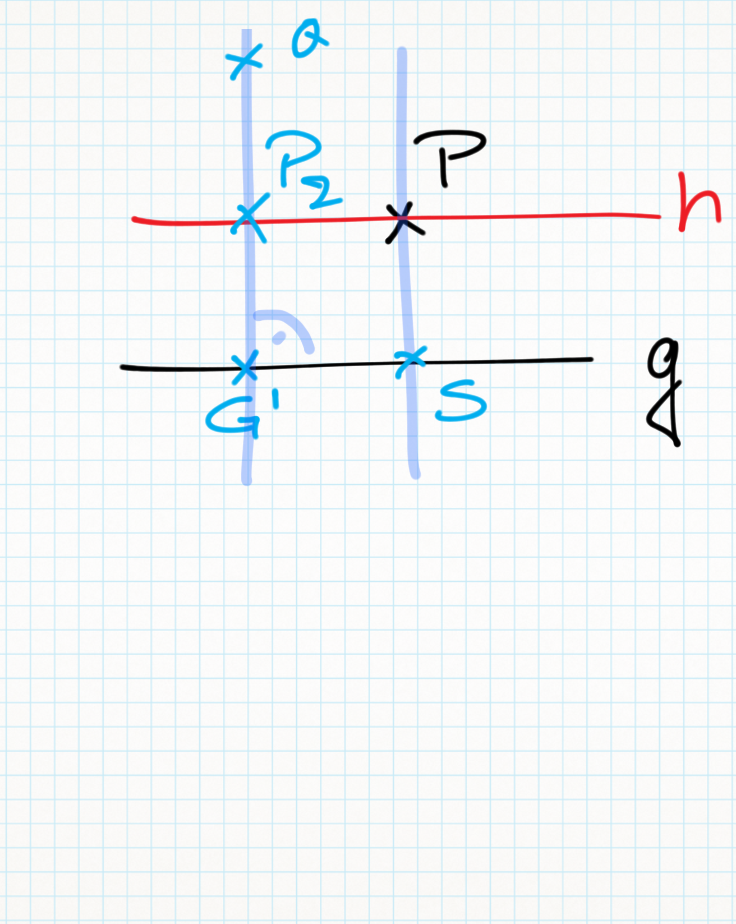
(3) Es gibt einen weiteren Punkt <math>G' \in g</math>mit<math>G' \neq S</math> // Vor., Axiom I.2<br />
 
(3) Es gibt einen weiteren Punkt <math>G' \in g</math>mit<math>G' \neq S</math> // Vor., Axiom I.2<br />
−
(4) Es gibt genau einen Strahl <math>G'Q+</math> in der HE G'S,P+ mit <math>\left| \angle SG'Q  \right| = 90</math> // Winkelkonstruktionsaxiom<br />
+
(4) Es gibt genau einen Strahl <math>\ G'Q^{+}</math> in der HE <math>\ G'S,P^{+}</math>  mit <math>\left| \angle SG'Q  \right| = 90</math> // Vor., (3), Winkelkonstruktionsaxiom<br />
−
(5) es gibt genau einen Punkt P_2 auf <math>G'Q+</math> mit <math>\left| SP \right| = \left| G'_2P_2 \right|</math> // Axiom v. Lineal, (4),(2)<br />
+
(5) Es gibt genau einen Punkt <math>P_2</math> auf <math>\ G'Q^{+}</math> mit <math>\left| SP \right| = \left| G'_2P_2 \right|</math> // Axiom v. Lineal, (4),(2)<br />
 
(6) <math>\exists h: P, P_2 \in h</math> // Vor., (5), Axiom I.1<br />
 
(6) <math>\exists h: P, P_2 \in h</math> // Vor., (5), Axiom I.1<br />
 
(7) qed?!? (oder muss noch bewiesen werden, dass alle Punkte der Geraden h denselben Abstand zur Geraden g haben?!? eigentlich trivial, oder? :-) )<br />--[[Benutzer:Nummero6|Tchu Tcha Tcha]] 15:20, 10. Jul. 2012 (CEST)
 
(7) qed?!? (oder muss noch bewiesen werden, dass alle Punkte der Geraden h denselben Abstand zur Geraden g haben?!? eigentlich trivial, oder? :-) )<br />--[[Benutzer:Nummero6|Tchu Tcha Tcha]] 15:20, 10. Jul. 2012 (CEST)

Aktuelle Version vom 10. Juli 2012, 15:59 Uhr


Satz XI. 1: (Existenz von Parallelen)
Zu jedem Punkt \ P außerhalb einer Geraden \ g gibt es eine Gerade \ h, die durch \ P geht und parallel zu \ g ist.
Beweis der Existenz von Parallelen

Übungsaufgabe


Lösungsversuch Nummero6/Tchu Tcha Tcha:
Parallel S1.png
Parallel S2.png

(1) Nach der Ex. & Eind. des Lots gibt es eine Gerade durch P, welche senkrecht zu g ist.
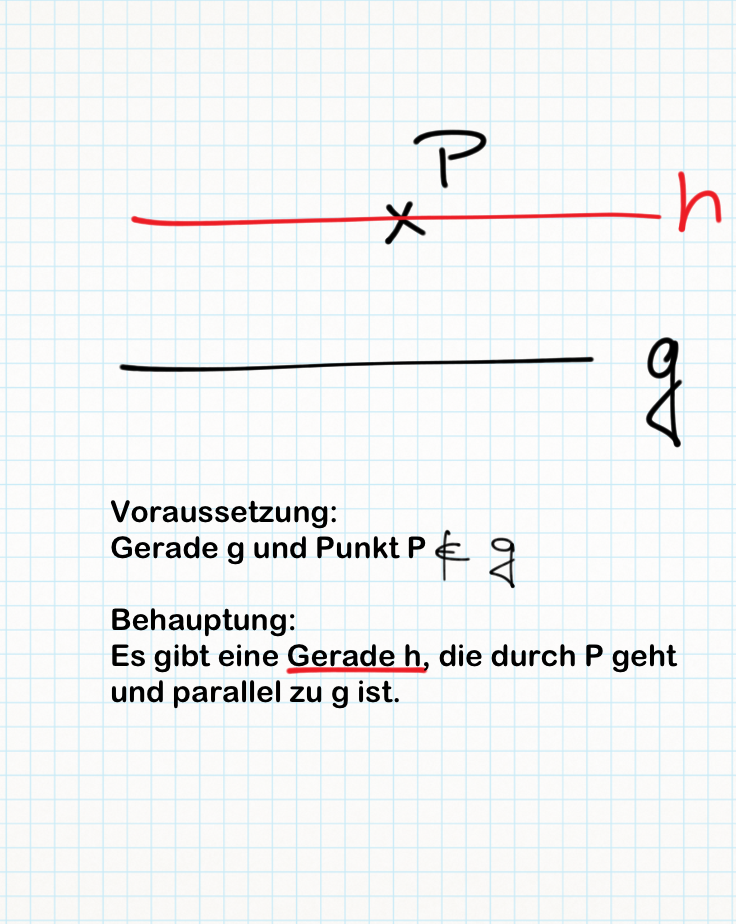
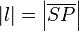(2) \left| l \right| = \left| \overline{SP} \right| // Vor., (1), Abstandsaxiom
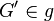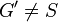(3) Es gibt einen weiteren Punkt G' \in gmitG' \neq S // Vor., Axiom I.2
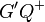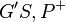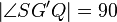(4) Es gibt genau einen Strahl \ G'Q^{+} in der HE \ G'S,P^{+} mit \left| \angle SG'Q \right| = 90 // Vor., (3), Winkelkonstruktionsaxiom
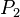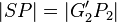(5) Es gibt genau einen Punkt P_2 auf \ G'Q^{+} mit \left| SP \right| = \left| G'_2P_2 \right| // Axiom v. Lineal, (4),(2)
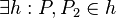(6) \exists h: P, P_2 \in h // Vor., (5), Axiom I.1
(7) qed?!? (oder muss noch bewiesen werden, dass alle Punkte der Geraden h denselben Abstand zur Geraden g haben?!? eigentlich trivial, oder? :-) )
--Tchu Tcha Tcha 15:20, 10. Jul. 2012 (CEST)


Die Eindeutigkeit ("Zu jedem Punkt \ P außerhalb einer Geraden \ g gibt es höchstens eine Gerade \ h, die durch \ P geht und parallel zu \ g ist.") kann in der absoluten Geometrie nicht bewiesen werden. Wir müssen die Eindeutigkeit der Parallelen axiomatisch fordern. Das entsprechende Axiom heißt Euklidisches Parallelenaxiom (EP). Sobald das EP gilt, befinden wir uns nichtmehr in der absoluten Geometrie, sondern in der euklidischen.

Von „http://geometrie.zum.de/index.php?title=Existenz_von_Parallelen_(SoSe_12)&oldid=16382“