Lösung Bierkasten-/Proseccobeweis (SoSe 12): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (→Bemerkungen M.G. zum Nachweis von F) |
*m.g.* (Diskussion | Beiträge) (→Der Nachweis von F) |
||
| Zeile 27: | Zeile 27: | ||
=== Der Nachweis von F === | === Der Nachweis von F === | ||
<ggb_applet width="1008" height="451" version="4.0" ggbBase64="UEsDBBQACAAIAISR6kAAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiu5QIAUEsHCEXM3l0aAAAAGAAAAFBLAwQUAAgACACEkepAAAAAAAAAAAAAAAAADAAAAGdlb2dlYnJhLnhtbO1c23Ibtxm+Tp4Cw2p6Ja5wBtaVktHBbj3jJJ7YzWQ6mfEslyC1EbnL7C4lyk0uMr1x36K3vWxOF+07+CH8JP0B7PJMiaQsS3bLiQwuzvi+/wQsmP1PR/0eOjd5kWTpQYMEuIFMGmftJO0eNIZlp6kbn37y8X7XZF3TyiPUyfJ+VB40uK2ZtA8aUnDKW7rVpC1BmjxqkWbIW50mkzQysqMjrEUDoVGRPEizz6O+KQZRbJ7Fp6YfPcniqHQDn5bl4MHe3sXFRVAPFWR5d6/bbQWjot1AMM20OGhUXx5AdzONLpirTjEme19/9sR330zSoozS2DSQXcIw+eTjj/YvkrSdXaCLpF2ewoIx5Q10apLuKSxKSFjUnq01AEQGJi6Tc1NA26lHt+iyP2i4alFqyz/y31BvvJ4GaifnSdvkBw0cUAAgyxOTllUpqUbZq9vvnyfmwndkv7kxYF5llvVake0Dff89ophitGsT4hMKiZS+CPs8zHxCfcJ9Inwd7ptzX5X7OtzX4ayBzpMiafXMQaMT9QoALUk7ORA2fi7Ky55x86kyJuslu7CmInkJlRkGED3KFl+8a/8k/HFcoTu1SDI1apkPNxy0HhJG0OuPSW+0UlYPSpetk4oV65RXDOoXvtZCxdSYMJT7z/0tjMiuWub8iP75ZgNK/k6WuL9X68p+pR6oOLV1K/EpTb+wCsNCJEIr9wQJUA6pQMwFIiEkiiJQB0QE4gIeiUbSpgoxBQUcMaSRrUcYctohNPzDletMIgGd2VwFSokIDMSRYIg4peIIVAk5xQQlpQxqCIEENLLDE2q7YBJxCU9MIw5ztDqpCFRk0BCeYXiKGEHMNiYKUYmk7Y9wq+tS26lDlxRJjCSxHYJag0p7dYb6GjG7GlnBlaSDYVlBVKEe99s1XGU2GGdDdbBIE0vnLdSMIfxovxe1TA+cwzNLJULnUc+qhBupk6UlqlmkPq+bR4PTJC6embKEVgX6NjqPnkSlGT2C2kU9tqsbZ2nxNM/K46w37KcFQnHWw/VE4TuZ+k4ni8l6bKqATxeIqQI59V0tHTeDEjQsDIyf5UVdPWq3H9saE9sAUH6R9i6PchOdDbJkdhn7e87P7Jth3EvaSZR+BdJqR7G4oInbsQardjucsnomWd5+dlmADKPRX0yeQU0WBpoyzsFTEaU1aPVlVRLigGgtNNh+gamk0GMRR1b7OA6YZkRhwTUXoQbNvFxepKQf2ZyPGYpGZrLYbm5Ve+rhcXGU9SZZbv3H0aAc5i5iAOuY20Udpt2ecTLi7C244/islY2eeeFgvq/nlwN4wn4Gra7DHYFxoAIcZrdKWz51dezUxrWwq4NdDVxLW9Iel5OQuhoubfnU1QLx9VOrlsrqZRJcD5MUzqThxqziOOG3zn2YJuWT+qFM4rNqqcQ3+HzYb5mxCM32Sd5Wn/t7czK2f2by1PQqkQYyh9mw8Bo6Je1tEyd9ePQFFSSRpevPMAGf2zbd3NQT77lozAPmSvG0sC5ku64e5Vn/cXr+HGRhbgL7e/Us94s4TwZW5lAL/MCZmUhVOykicCPt6XZWB2HpsXUXAE9poQHtHJanWe7iLTAqkFrV65k+xFqodOLlJHQM87EL2yyeKGt9C3Zt7Pt8+YQwKF4qak4oo97gNLKhXbXoXnRp8hkYXH+fZe15cAB7twLQ8YHtwLI7MMYLhp8xfBlAh06fZswU4F2gEQhsICiWWjNFccgwCUGCL222tAGgz6TM2oOXPqT3Ia0FwirgjNH2uXMsgmh5DK9B8+gFWcRzVq7fMaDbwKnsVgbwozZ9C4jFWb8fpW2Uusjny+iyMfHDEbYyiCLiwfPADMu6KHrBfG9VHwv459BbDa2tfLU0Ty13Ffp4e+wnCJI5yVNhJZBchYwQCRlYhhorh2+T6ICGeiy/VMh5w1xCzHAGW6PCeY+y8hPuy5+Sdtu4gNE7ru9S36Tw1jLpD3pJnJRjaHuW+cdpCbbTOOOxaBLPjBlYX/RF+jyP0sJucX2dKVO7lj4cfxD6QO9GH46X6ENrfW1o3W9daJIlRtsqA7iAUEsIxBTEeFpCZKbfI22Y5fap04ZZdiuTNkPr0dW0zjmZrVw2oT6GdOl90KowoJyKMIRoXDKOtXZigYNQ2AheEBAICgKgbkHlltHSWiDlcBNSDt85KV90OoUpLZJN6u1TU942ZyRgYcjBU1HFQsJwKNzAkC2t1xJMKdDlUPBbIO04yeOeWW4qDxfIi68mD4LnJB6TE1/npG7XVm5l2JKuSc9hqrAzR2iEq6PqS+zHRy/rnBFxNtWWkSrrJZniBmQiT0bosK5/WNc6pPbsKdAh02CQiQKLLJmEfFYNccih52Wh96FwBfPB91KDbM9Skk4Sb8/90QL37U24b/+f++XcNwkPGNOCMKkIpZgrcTfkj73zHP9tz/+i4X7oCzYx3w+3Mt/2hLfrk5ZPNrfdhK1huycWGOhUIWweFAHXCFpJqW8OfhPUlHHGOaNCafuO6a2b4FVMxB7wZZHNyeZcnLxbLq4AW4ICYE5AAzBASqiqtgGwhVOKaa0IE1poeSshSu+ym6VzQFeSbS0ftUDNo/1VAv3FZ8RX6/pqHUiYZYdcx4IfssZ53Nm2dmrjvYcgjkObLARDZBMSV+9PC9O1T+OZdLfbJV01063FrckDCUZUESGYpJoQ6cMrsMOQKwQPsVZcceJ1GwdCWm2H4FGAQRCYv0f7pKtZ6dwjViC4xZpKxiglUnIZ0soKaByC+Q215uAksa6OcniglKI6BK8H1kF8MJREy45y7owUFtCQKeCFES6J5KryoiogNORK23M2+54n9KyABklwl0JDq5DB533iZR3HMN4HOYu/GBJXtpz6au0XxFeMXtDKOWzlGui7cw0Qf64IuNntOIb2tvK+eqZbSzsNqAiVtlGfCEGEqfcLTQrSTkgI+22uMFGkPkCjShFJKWzHNeVcfDh+wcrrfSEFBxwDuPbgQyl3XulIUYHmEB8SIhTlQERlgQgJKONS8ZBILWUoyYdDyr2hBBQCPDRlgK9iErZJ1VGzCBQlIcRTECpxgqXnhMFIsGPSGHKsZmH2HlGy3sYsekHqrRld8AmPNtmUPbqzDXL1LpesJwLEnlqA7eNgKLkAs+lbC9A+CJFDHiouIDJzAkB1AHYSBIARDOyLULzFDZy78DFHx6MZL328wMjrf11NibtKMIYcatv2MJlhPaVASy3A6nAqaUioVlt6W3+4RfCibl69DZuiTVRn0kwvJW7h6sn6uhbl8RQ59el2r5ddfGk6PTNyyK+rOctoqoKpE0/To0WaftqIpp+upUkvoWn9t6Q3oYnULNH3jqVKmR56lhbfALz+eSOWfl5kiWkO4ZOEuAu23HgpS+9GmaTfcbL3jqOT+oh+lSb9shFHv2zF0bvRpCZRVzmqu2PJjAY5DGNf/FUQPDejEjwgFBw0fv/dMCv/8E3LlJH/6prPslBC/cZs4xsowo3jvaR4Ej03X8+uuLptW5g86YxvV7vLlbhRB2X13rOM8tK9AkaOOBVwpgSurxyoisdAM0H96wshNJl5pXk9vvQm+G65ybm3+Nooe3y5icgKX8yJfZPhYa9CsiX4vgV//etGVubXrfz1bXqC+2BGrqfh8JqXE69/24iG3+ZpIIGGDxaUQcAeElHfkvufomG5tREz1ub1z+ubGvFBmRoewF6eivENS14d1YcYBKbKU9X2f21TLmfA3UHfuNWinfVBlh8UyCrQsI8Gl8hCAYZd6eoOkNDhlJnndDOU1Y1RVh80ynVUokiIJyjLzUBmMyBvEJHc7cXqRWywGAdmDKSulkDJVZUHmFUXStcGh28LDr9X4MgAfKQXGicmoraBVEo1jrfYhvGsngGntT44+l6BowKKib10Wn34+F0u1bL2G2rTYD/cFpzwTsG53jatRJFQNfkdgyL1PQUI6THmNZArUVyIJYe9KD9KCnelbS6q7NR3WebDSeMLTq8OKm2INobT3O1dv5lbXATMuwLbReCL1jaYra4/a/sbRsVDpTiTyhv4JkioVu6sAxAXWNQnu2/7XcXqtz4zQJ7eIyAXAbtcBfBLK6OEU02kfT8gOFiA28dxVtqfWByXnpI9XBDxZAPZTm5iSohgjhN7SeN+X84Qb0m2lx+KzZ6K7ZDgzau/dR+c7D588+pVdwf5zx9NHsHa28M8PkUnaAjUPvz97wiGoJUGJ1Dz+OjNj/9GtrrPZoFtf3j85sf/7PgcHnTfvPrnN9m5ye0q/3p4/MPBN6Y/KC8LU9bjIER26S7zLcRci6PjH978/R9L2qBxEzk/yNGqJnxX7KLDUZL10Tkg8jQq4tMNTgPv/XFg/UP1tSJv+yO9iWuzr+pri2J/cy4n7m21f1shXXhGurobIIzvUxClgzBkdBwtyfo+HIBFJ+gwsSE6syemJ4lBz8rcxGcG7Uxk+OThDzsIpDM1SduUoGMz4r2Dkj56OkzPSvQo2ADee3/euqEAM0qFHksqq8wvuD4h+GQLoFYRtDf903L7XP8fiD75L1BLBwiQfDPdRw0AAB5JAABQSwECFAAUAAgACACEkepARczeXRoAAAAYAAAAFgAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAAIAISR6kCQfDPdRw0AAB5JAAAMAAAAAAAAAAAAAAAAAF4AAABnZW9nZWJyYS54bWxQSwUGAAAAAAIAAgB+AAAA3w0AAAAA" showResetIcon = "false" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /> | <ggb_applet width="1008" height="451" version="4.0" ggbBase64="UEsDBBQACAAIAISR6kAAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiu5QIAUEsHCEXM3l0aAAAAGAAAAFBLAwQUAAgACACEkepAAAAAAAAAAAAAAAAADAAAAGdlb2dlYnJhLnhtbO1c23Ibtxm+Tp4Cw2p6Ja5wBtaVktHBbj3jJJ7YzWQ6mfEslyC1EbnL7C4lyk0uMr1x36K3vWxOF+07+CH8JP0B7PJMiaQsS3bLiQwuzvi+/wQsmP1PR/0eOjd5kWTpQYMEuIFMGmftJO0eNIZlp6kbn37y8X7XZF3TyiPUyfJ+VB40uK2ZtA8aUnDKW7rVpC1BmjxqkWbIW50mkzQysqMjrEUDoVGRPEizz6O+KQZRbJ7Fp6YfPcniqHQDn5bl4MHe3sXFRVAPFWR5d6/bbQWjot1AMM20OGhUXx5AdzONLpirTjEme19/9sR330zSoozS2DSQXcIw+eTjj/YvkrSdXaCLpF2ewoIx5Q10apLuKSxKSFjUnq01AEQGJi6Tc1NA26lHt+iyP2i4alFqyz/y31BvvJ4GaifnSdvkBw0cUAAgyxOTllUpqUbZq9vvnyfmwndkv7kxYF5llvVake0Dff89ophitGsT4hMKiZS+CPs8zHxCfcJ9Inwd7ptzX5X7OtzX4ayBzpMiafXMQaMT9QoALUk7ORA2fi7Ky55x86kyJuslu7CmInkJlRkGED3KFl+8a/8k/HFcoTu1SDI1apkPNxy0HhJG0OuPSW+0UlYPSpetk4oV65RXDOoXvtZCxdSYMJT7z/0tjMiuWub8iP75ZgNK/k6WuL9X68p+pR6oOLV1K/EpTb+wCsNCJEIr9wQJUA6pQMwFIiEkiiJQB0QE4gIeiUbSpgoxBQUcMaSRrUcYctohNPzDletMIgGd2VwFSokIDMSRYIg4peIIVAk5xQQlpQxqCIEENLLDE2q7YBJxCU9MIw5ztDqpCFRk0BCeYXiKGEHMNiYKUYmk7Y9wq+tS26lDlxRJjCSxHYJag0p7dYb6GjG7GlnBlaSDYVlBVKEe99s1XGU2GGdDdbBIE0vnLdSMIfxovxe1TA+cwzNLJULnUc+qhBupk6UlqlmkPq+bR4PTJC6embKEVgX6NjqPnkSlGT2C2kU9tqsbZ2nxNM/K46w37KcFQnHWw/VE4TuZ+k4ni8l6bKqATxeIqQI59V0tHTeDEjQsDIyf5UVdPWq3H9saE9sAUH6R9i6PchOdDbJkdhn7e87P7Jth3EvaSZR+BdJqR7G4oInbsQardjucsnomWd5+dlmADKPRX0yeQU0WBpoyzsFTEaU1aPVlVRLigGgtNNh+gamk0GMRR1b7OA6YZkRhwTUXoQbNvFxepKQf2ZyPGYpGZrLYbm5Ve+rhcXGU9SZZbv3H0aAc5i5iAOuY20Udpt2ecTLi7C244/islY2eeeFgvq/nlwN4wn4Gra7DHYFxoAIcZrdKWz51dezUxrWwq4NdDVxLW9Iel5OQuhoubfnU1QLx9VOrlsrqZRJcD5MUzqThxqziOOG3zn2YJuWT+qFM4rNqqcQ3+HzYb5mxCM32Sd5Wn/t7czK2f2by1PQqkQYyh9mw8Bo6Je1tEyd9ePQFFSSRpevPMAGf2zbd3NQT77lozAPmSvG0sC5ku64e5Vn/cXr+HGRhbgL7e/Us94s4TwZW5lAL/MCZmUhVOykicCPt6XZWB2HpsXUXAE9poQHtHJanWe7iLTAqkFrV65k+xFqodOLlJHQM87EL2yyeKGt9C3Zt7Pt8+YQwKF4qak4oo97gNLKhXbXoXnRp8hkYXH+fZe15cAB7twLQ8YHtwLI7MMYLhp8xfBlAh06fZswU4F2gEQhsICiWWjNFccgwCUGCL222tAGgz6TM2oOXPqT3Ia0FwirgjNH2uXMsgmh5DK9B8+gFWcRzVq7fMaDbwKnsVgbwozZ9C4jFWb8fpW2Uusjny+iyMfHDEbYyiCLiwfPADMu6KHrBfG9VHwv459BbDa2tfLU0Ty13Ffp4e+wnCJI5yVNhJZBchYwQCRlYhhorh2+T6ICGeiy/VMh5w1xCzHAGW6PCeY+y8hPuy5+Sdtu4gNE7ru9S36Tw1jLpD3pJnJRjaHuW+cdpCbbTOOOxaBLPjBlYX/RF+jyP0sJucX2dKVO7lj4cfxD6QO9GH46X6ENrfW1o3W9daJIlRtsqA7iAUEsIxBTEeFpCZKbfI22Y5fap04ZZdiuTNkPr0dW0zjmZrVw2oT6GdOl90KowoJyKMIRoXDKOtXZigYNQ2AheEBAICgKgbkHlltHSWiDlcBNSDt85KV90OoUpLZJN6u1TU942ZyRgYcjBU1HFQsJwKNzAkC2t1xJMKdDlUPBbIO04yeOeWW4qDxfIi68mD4LnJB6TE1/npG7XVm5l2JKuSc9hqrAzR2iEq6PqS+zHRy/rnBFxNtWWkSrrJZniBmQiT0bosK5/WNc6pPbsKdAh02CQiQKLLJmEfFYNccih52Wh96FwBfPB91KDbM9Skk4Sb8/90QL37U24b/+f++XcNwkPGNOCMKkIpZgrcTfkj73zHP9tz/+i4X7oCzYx3w+3Mt/2hLfrk5ZPNrfdhK1huycWGOhUIWweFAHXCFpJqW8OfhPUlHHGOaNCafuO6a2b4FVMxB7wZZHNyeZcnLxbLq4AW4ICYE5AAzBASqiqtgGwhVOKaa0IE1poeSshSu+ym6VzQFeSbS0ftUDNo/1VAv3FZ8RX6/pqHUiYZYdcx4IfssZ53Nm2dmrjvYcgjkObLARDZBMSV+9PC9O1T+OZdLfbJV01063FrckDCUZUESGYpJoQ6cMrsMOQKwQPsVZcceJ1GwdCWm2H4FGAQRCYv0f7pKtZ6dwjViC4xZpKxiglUnIZ0soKaByC+Q215uAksa6OcniglKI6BK8H1kF8MJREy45y7owUFtCQKeCFES6J5KryoiogNORK23M2+54n9KyABklwl0JDq5DB533iZR3HMN4HOYu/GBJXtpz6au0XxFeMXtDKOWzlGui7cw0Qf64IuNntOIb2tvK+eqZbSzsNqAiVtlGfCEGEqfcLTQrSTkgI+22uMFGkPkCjShFJKWzHNeVcfDh+wcrrfSEFBxwDuPbgQyl3XulIUYHmEB8SIhTlQERlgQgJKONS8ZBILWUoyYdDyr2hBBQCPDRlgK9iErZJ1VGzCBQlIcRTECpxgqXnhMFIsGPSGHKsZmH2HlGy3sYsekHqrRld8AmPNtmUPbqzDXL1LpesJwLEnlqA7eNgKLkAs+lbC9A+CJFDHiouIDJzAkB1AHYSBIARDOyLULzFDZy78DFHx6MZL328wMjrf11NibtKMIYcatv2MJlhPaVASy3A6nAqaUioVlt6W3+4RfCibl69DZuiTVRn0kwvJW7h6sn6uhbl8RQ59el2r5ddfGk6PTNyyK+rOctoqoKpE0/To0WaftqIpp+upUkvoWn9t6Q3oYnULNH3jqVKmR56lhbfALz+eSOWfl5kiWkO4ZOEuAu23HgpS+9GmaTfcbL3jqOT+oh+lSb9shFHv2zF0bvRpCZRVzmqu2PJjAY5DGNf/FUQPDejEjwgFBw0fv/dMCv/8E3LlJH/6prPslBC/cZs4xsowo3jvaR4Ej03X8+uuLptW5g86YxvV7vLlbhRB2X13rOM8tK9AkaOOBVwpgSurxyoisdAM0H96wshNJl5pXk9vvQm+G65ybm3+Nooe3y5icgKX8yJfZPhYa9CsiX4vgV//etGVubXrfz1bXqC+2BGrqfh8JqXE69/24iG3+ZpIIGGDxaUQcAeElHfkvufomG5tREz1ub1z+ubGvFBmRoewF6eivENS14d1YcYBKbKU9X2f21TLmfA3UHfuNWinfVBlh8UyCrQsI8Gl8hCAYZd6eoOkNDhlJnndDOU1Y1RVh80ynVUokiIJyjLzUBmMyBvEJHc7cXqRWywGAdmDKSulkDJVZUHmFUXStcGh28LDr9X4MgAfKQXGicmoraBVEo1jrfYhvGsngGntT44+l6BowKKib10Wn34+F0u1bL2G2rTYD/cFpzwTsG53jatRJFQNfkdgyL1PQUI6THmNZArUVyIJYe9KD9KCnelbS6q7NR3WebDSeMLTq8OKm2INobT3O1dv5lbXATMuwLbReCL1jaYra4/a/sbRsVDpTiTyhv4JkioVu6sAxAXWNQnu2/7XcXqtz4zQJ7eIyAXAbtcBfBLK6OEU02kfT8gOFiA28dxVtqfWByXnpI9XBDxZAPZTm5iSohgjhN7SeN+X84Qb0m2lx+KzZ6K7ZDgzau/dR+c7D588+pVdwf5zx9NHsHa28M8PkUnaAjUPvz97wiGoJUGJ1Dz+OjNj/9GtrrPZoFtf3j85sf/7PgcHnTfvPrnN9m5ye0q/3p4/MPBN6Y/KC8LU9bjIER26S7zLcRci6PjH978/R9L2qBxEzk/yNGqJnxX7KLDUZL10Tkg8jQq4tMNTgPv/XFg/UP1tSJv+yO9iWuzr+pri2J/cy4n7m21f1shXXhGurobIIzvUxClgzBkdBwtyfo+HIBFJ+gwsSE6syemJ4lBz8rcxGcG7Uxk+OThDzsIpDM1SduUoGMz4r2Dkj56OkzPSvQo2ADee3/euqEAM0qFHksqq8wvuD4h+GQLoFYRtDf903L7XP8fiD75L1BLBwiQfDPdRw0AAB5JAABQSwECFAAUAAgACACEkepARczeXRoAAAAYAAAAFgAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAAIAISR6kCQfDPdRw0AAB5JAAAMAAAAAAAAAAAAAAAAAF4AAABnZW9nZWJyYS54bWxQSwUGAAAAAAIAAgB+AAAA3w0AAAAA" showResetIcon = "false" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /> | ||
| + | |||
| + | --[[Benutzer:Oz44oz|Oz44oz]] 18:14, 10. Jul. 2012 (CEST) | ||
| + | |||
===Bemerkungen M.G. zum Nachweis von F=== | ===Bemerkungen M.G. zum Nachweis von F=== | ||
Version vom 10. Juli 2012, 21:43 Uhr
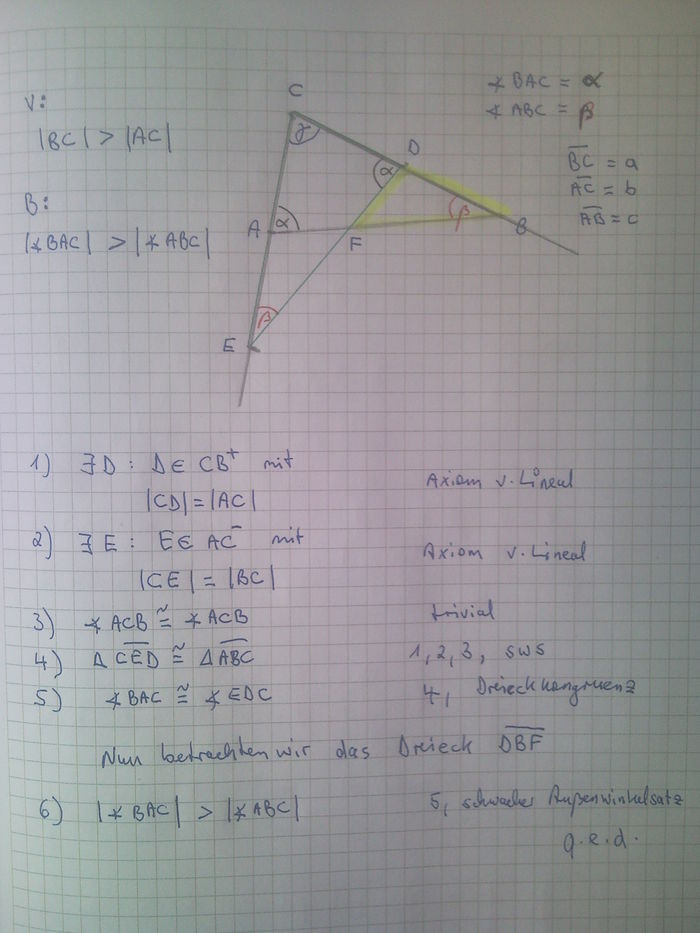
In der Vorlesung haben wir den Satz "Im Dreieck liegt der größeren Seite der größere Winkel gegenüber" beweisen, indem wir die zwei kongruenten Winkel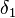 
und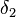 
zur Hilfe genommen haben.
Beweisen Sie den Satz, indem Sie 
und 
direkt miteinander vergleichen, also vergleichen Sie sie ohne Hilfswinkel.
Sie können mit diesem Beweis einen Bierkasten/ Prosecco gewinnen. Die erste korrekte Lösung im wiki gewinnt!
Inhaltsverzeichnis |
Lösungsvorschlag von oz44oz und annap.
--Oz44oz 15:53, 9. Jul. 2012 (CEST)
Bemerkung M.G. zum Lösungsvorschlag von oz44oz und annap
Fast perfekt.
Warum entsteht das Dreieck Fehler beim Parsen(Unbekannte Funktion „\overlin“): \overlin{FBD}
? Einfacher: warum liegt der Punkt 
dort, wo er liegt?--*m.g.* 16:17, 9. Jul. 2012 (CEST)
Weitere Bemerkungen:
Oh man, wie einfach... und ich komme nicht drauf.
@ ozz44oz: Betrachten wir nicht das Dreieck EAF? Weil dann würde doch der Außenwinkelsatz greifen, und Alpha wäre größer als Beta.
Und da entsteht ein Viereck AFDC. Sind da die beiden Alphas gleich?--RitterSport 21:46, 9. Jul. 2012 (CEST)
noch mal M.G.
Mit dem Dreieck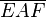 
geht es natürlich auch. Die Dreiecke sind aber nur dann relevant für den Beweis, wenn auf der offenen Strecke 
liegt. Der Nachweis bleibt. Die 's sind natürlich kongruent, da ja die Kongruenz der Dreiecke 
und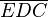 
nachgewiesen wurde.--*m.g.* 23:24, 9. Jul. 2012 (CEST)
Der Nachweis von F
--Oz44oz 18:14, 10. Jul. 2012 (CEST)
