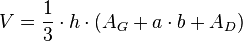Körpermodelle: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(→Pyramidenstumpf) |
|||
| Zeile 26: | Zeile 26: | ||
<iframe src="http://www.ph-heidelberg.de/wp/gieding/flashz/Koerper/Pyramidenstumpf_03.swf" width="1000" height="600" frameborder="2"></iframe> | <iframe src="http://www.ph-heidelberg.de/wp/gieding/flashz/Koerper/Pyramidenstumpf_03.swf" width="1000" height="600" frameborder="2"></iframe> | ||
| + | |||
| + | ===Grundfläche=== | ||
| + | <math>A_G=a^2</math> | ||
| + | |||
| + | ===Deckfläche=== | ||
| + | <math>A_D=b^2</math> | ||
| + | |||
===Mantelfläche=== | ===Mantelfläche=== | ||
<math>A_M =2 \cdot (a + b) \cdot h</math> | <math>A_M =2 \cdot (a + b) \cdot h</math> | ||
| − | |||
===Oberfläche=== | ===Oberfläche=== | ||
Version vom 17. Juli 2012, 12:11 Uhr
Inhaltsverzeichnis |
Aus dem Sommersemester 2012
Die folgenden Modelle wurden im Sommersemester 2012 von den Studierenden der Veranstaltung Erstellen von Multimediaanwendungen für den Unterricht generiert.
Ikosaeder
[ www.ph-heidelberg.de is not an authorized iframe site ]
Änderung der Drehrichtung: Ziehen mit der Maus über die App.
Oktaeder
[ www.ph-heidelberg.de is not an authorized iframe site ]
Änderung der Drehrichtung: Ziehen mit der Maus über die App.
6-seitiges Prisma
[ www.ph-heidelberg.de is not an authorized iframe site ]
4-seitige Pyramide
[ www.ph-heidelberg.de is not an authorized iframe site ]
Pyramidenstumpf
quadratischer Pyramidenstumpf
[ www.ph-heidelberg.de is not an authorized iframe site ]
Grundfläche
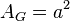
Deckfläche
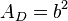
Mantelfläche
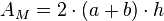
Oberfläche
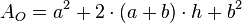
Volumen
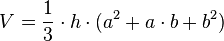
regelmäiger sechseckiger Pyramidenstumpf
[ www.ph-heidelberg.de is not an authorized iframe site ]
Grundfläche
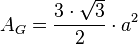
Deckfläche
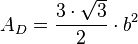
Mantelfläche
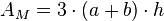
Oberfläche
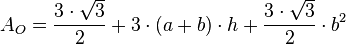
Volumen