Lösung Aufgabe 2.1 WS 12 13: Unterschied zwischen den Versionen
Caro44 (Diskussion | Beiträge) (→Aufgabe 2.1) |
Caro44 (Diskussion | Beiträge) (→Lösung von Caro44) |
||
| Zeile 28: | Zeile 28: | ||
--[[Benutzer:Caro44|Caro44]] 13:30, 7. Nov. 2012 (CET) | --[[Benutzer:Caro44|Caro44]] 13:30, 7. Nov. 2012 (CET) | ||
[[Kategorie: Lösung Aufgabe 2.1]] | [[Kategorie: Lösung Aufgabe 2.1]] | ||
| + | |||
| + | |||
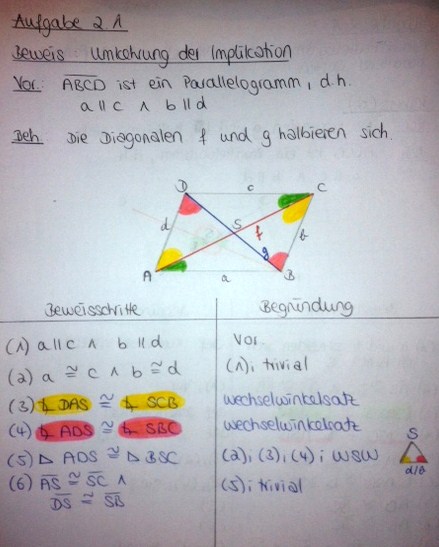
| + | (e) | ||
| + | [[Datei:Caro44_Beweis_Parallelogramm_Umkehrung.JPG]] | ||
| + | --[[Benutzer:Caro44|Caro44]] 14:49, 7. Nov. 2012 (CET) | ||
==Lösung von User: B.....== | ==Lösung von User: B.....== | ||
Aktuelle Version vom 7. November 2012, 14:49 Uhr
Aufgabe 2.1Der Begriff Parallelogramm sei als Viereck mit zwei Paaren paralleler Seiten definiert. Wir betrachten die folgende Implikation (I): (I) Wenn sich in einem Viereck die Diagonalen halbieren, dann ist das Viereck ein Parallelogramm. (a) Nennen Sie die Voraussetzung und die Behauptung der Implikation (I).
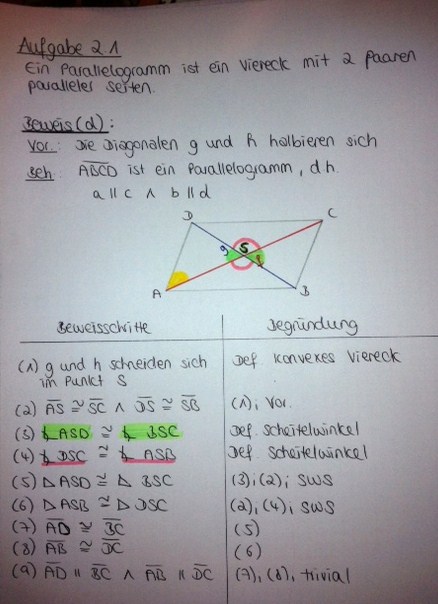
Lösung von Caro44(d)
Lösung von User: B.....a: Vor.: Die Diagonalen eines Vierecks halbieren sich. Lösung von User: YellowUnd hier noch was zu schmunzel und warum es so wichtig ist sauber zu definieren. Viel Spaß http://www.youtube.com/watch?v=3Fe-a2gUccs
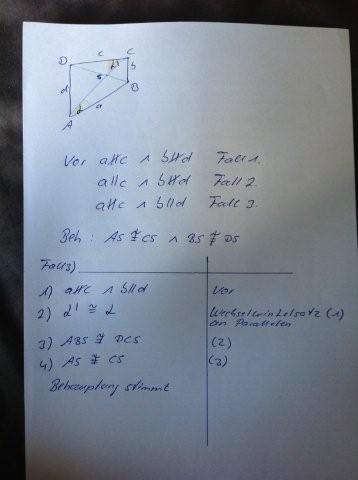
b)Vor: ABCD ist Parallelogramm c) Vor: ABCD ist kein Parallegramm
f)Wenn sich in einem Viereck die Diaganaolen halbieren genau dann ist es ein Parallelogramm Bemerkungen m.g.YoutubevideoDa halt ich mich besser raus, meine Frau schaut manchmal, was ich hier so schreibe.--*m.g.* 23:39, 6. Nov. 2012 (CET)
|