Quiz der Woche 4 (WS 12 13): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(Die Seite wurde neu angelegt: „{| class="wikitable" |- | <quiz> { Die nebenstehende Abbildung ist im Rahmen der Donnerstags-Veranstaltung: "Vorbereitung auf die Klausur mit Hilfe eines Classr…“) |
|||
| Zeile 36: | Zeile 36: | ||
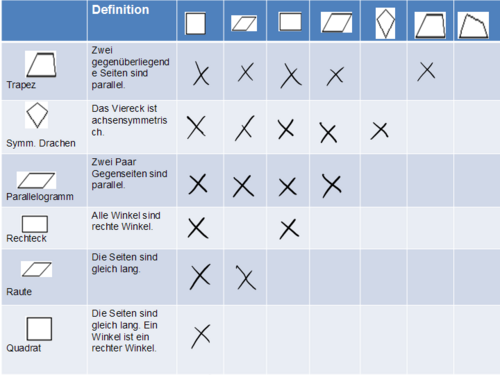
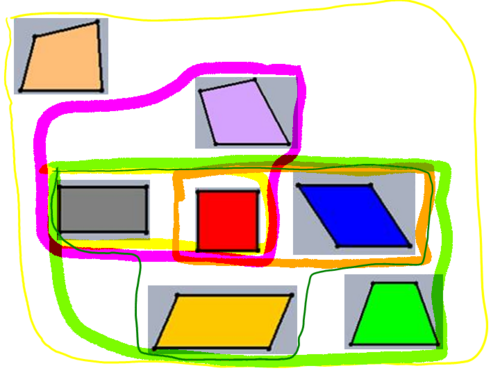
|| Ja, da jedes Quadrat auch ein Rechteck ist. | || Ja, da jedes Quadrat auch ein Rechteck ist. | ||
- Die pinkfarbene Linie gibt die Teilmengenbeziehungen des Drachens korrekt wieder. | - Die pinkfarbene Linie gibt die Teilmengenbeziehungen des Drachens korrekt wieder. | ||
| − | || Da Rechtecke nicht achsensymmetrisch sind, ist dies leider nicht korrekt. | + | || Da Rechtecke bezüglich ihrer Diagonalen nicht achsensymmetrisch sind, ist dies leider nicht korrekt. |
+ Alle Figuren, die dick grün umrandet sind lassen sich den Trapezen zuordnen. | + Alle Figuren, die dick grün umrandet sind lassen sich den Trapezen zuordnen. | ||
|| Ja, das ist korrekt! | || Ja, das ist korrekt! | ||
Version vom 22. November 2012, 17:10 Uhr
|
|
|
| |
|
| |
|

