Pfeilklassen 2012 13: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (→Addition von Pfeilklassen) |
Jessy* (Diskussion | Beiträge) (→Satz P.1) |
||
| Zeile 14: | Zeile 14: | ||
==Eigenschaften== | ==Eigenschaften== | ||
===Satz P.1=== | ===Satz P.1=== | ||
| − | :Die Relation parallelgleich ist eine ÄR auf der Menge der Pfeile des Raumes bzw. der Ebene. | + | :Die Relation parallelgleich ist eine ÄR auf der Menge der Pfeile des Raumes bzw. der Ebene.<br /><br /> |
| + | <u>Zu zeigen:</u><br /> | ||
| + | a) Reflexivität<br /> | ||
| + | b) Symmetrie<br /> | ||
| + | c) Transitivität<br /><br /> | ||
| + | --[[Benutzer:Jessy*|Jessy*]] 17:08, 11. Dez. 2012 (CET) | ||
| + | |||
==Definition Pfeilklasse== | ==Definition Pfeilklasse== | ||
{{Definition|P.2 (Pfeilklasse) <br />Eine Pfeilklasse des Raumes bzw. der Ebene ist eine Äquivalenzklasse nach der Relation ''parallelgleich'' auf der menge der Pfeile des Raumes bzw. der Ebene.}} | {{Definition|P.2 (Pfeilklasse) <br />Eine Pfeilklasse des Raumes bzw. der Ebene ist eine Äquivalenzklasse nach der Relation ''parallelgleich'' auf der menge der Pfeile des Raumes bzw. der Ebene.}} | ||
Version vom 11. Dezember 2012, 17:08 Uhr
PfeileUnter einem Pfeil versteht man eine gerichtete Strecke. Wir werden den begriff intuitiv gebrauchen. PfeilklassenDefinition parallelgleichDefinition P.1 (parallelgleich)
EigenschaftenSatz P.1
Zu zeigen: Definition PfeilklasseDefinition P.2 (Pfeilklasse) Addition von PfeilklassenDefinition der Addition von PfeilklassenDefinition P.3 (Addition auf der Menge der Pfeilklassen) |
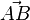und 
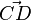heißen parallelgleich, wenn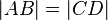 
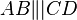
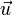und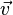 
zwei Pfeilklassen. Ferner seien
