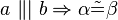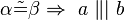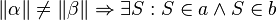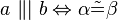Lösung von Aufgabe 3.3 (WS 12 13 P): Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
Zeile 8: Zeile 8:
 
zu a) Stufenwinkel an geschnittenen Parallelen sind kongruent zueinander. --[[Benutzer:Der Bohrer|Der Bohrer]] 11:16, 22. Nov. 2012 (CET)
 
zu a) Stufenwinkel an geschnittenen Parallelen sind kongruent zueinander. --[[Benutzer:Der Bohrer|Der Bohrer]] 11:16, 22. Nov. 2012 (CET)
  
 +
Zu b)
 +
 +
1. Stufenwinkelsatz
 +
 +
2. Umkehrung Stufenwinkelsatz
 +
 +
3. Die Geraden wären identisch somit trotzdem paralell und somit existieren die Winkel nicht, beziehungsweise es währen Nebenwinkel.
 +
 +
4. Äquivalentsaussage des Stufenwinkelsatzes
  
 
[[Category:Einführung_P]]
 
[[Category:Einführung_P]]

Version vom 3. Februar 2013, 13:29 Uhr

a) Wie lautet der Stufenwinkelsatz? (schauen Sie bei Bedarf in Schulbüchern nach).
b) Es seien a und b zwei nichtidentische Geraden, die durch eine dritte Gerade c jeweils in genau einem Punkt geschnitten werden. Bei diesem Schnitt entstehen die Stufenwinkel \alpha und \beta . Welche der folgenden Aussagen repräsentiert den Stufenwinkelsatz bzw. ist eine zu diesem Satz äuivalente Aussage (Begründen Sie jeweils)?

  1. \ a \ \|| \ b \Rightarrow \alpha \tilde {=} \beta
  2. \alpha \tilde {=} \beta \Rightarrow \ a \ \|| \ b
  3. \|\alpha \|\not= \| \beta \| \Rightarrow \exists S: S \in a \wedge S \in b
  4. \ a \ \|| \ b \Leftrightarrow \alpha \tilde {=} \beta

zu a) Stufenwinkel an geschnittenen Parallelen sind kongruent zueinander. --Der Bohrer 11:16, 22. Nov. 2012 (CET)

Zu b)

1. Stufenwinkelsatz

2. Umkehrung Stufenwinkelsatz

3. Die Geraden wären identisch somit trotzdem paralell und somit existieren die Winkel nicht, beziehungsweise es währen Nebenwinkel.

4. Äquivalentsaussage des Stufenwinkelsatzes

Von „http://geometrie.zum.de/index.php?title=Lösung_von_Aufgabe_3.3_(WS_12_13_P)&oldid=21337“