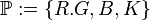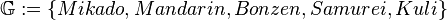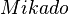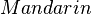Lösung von Aufgabe 5.2 S (WS 12 13): Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(→‎Lösung von User...)
(→‎Lösung von User Caro44)
Zeile 34: Zeile 34:
  
 
==Lösung von User Caro44==
 
==Lösung von User Caro44==
 +
 +
 +
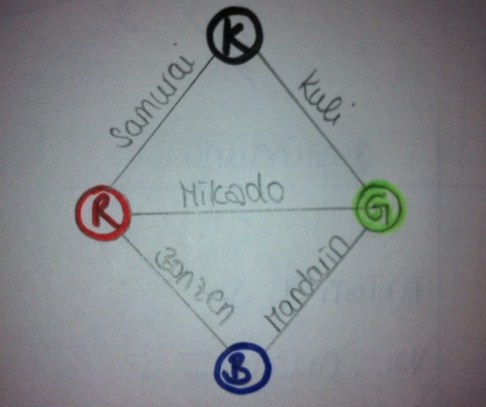
'''a) Skizze'''
 +
[[Datei:Caro44_Skizze.JPG]]
 +
  
  

Version vom 27. November 2012, 12:10 Uhr


Aufgabe 5.2

Gegeben seien eine rote Kugel aus Knete (R), eine blaue Kugel aus Knete (B), eine grüne Kugel aus Knete (G) und eine schwarze Kugel aus Knete (K). Aus einem Mikadospiel wurde jeweils genau ein Repräsentant der folgenden Stäbchenart entnommen: Mikado, Mandarin, Bonzen und Samurai.
Wir betrachten das folgende Modell für die Inzidenz:

  • Menge aller Punkte \mathbb{P}:=\{R. G, B, K\}
  • Menge aller Geraden \mathbb{G}:=\{Mikado, Mandarin, Bonzen, Samurei, Kuli\}

Die Inzidenzrelation interpretieren wir wie folgt: Ein Modellpunkt inziert mit einer Modellgeraden, wenn der Modellpunkt auf die Modellgerade gesteckt wurde.
Wir lassen die Modellpunkte mit den Modellgeraden jetzt wie folgt inzidieren:

  • R und G inzidieren mit Mikado
  • G und B inzidieren mit Mandarin
  • B und R inzidieren mit Bonzen
  • R und K inzidieren mit Samurai
  • G und K inzidieren mit Kuli
(a) Fertigen Sie eine Skizze für dieses Modell an bzw. stellen Sie ein Foto von einem real gebauten Modell hier ein.
(b) Nennen Sie drei verschiedene Gründe, warum dieses Modell kein Modell für die Inzidenzaxiome des Raumes ist.
(c) Ergänzen Sie das Modell Sie derart, dass die Inzidenzaxiome I.1 bis I.7 erfüllt sind.
(d) Mit dem von Ihnen ergänzten Modell haben Sie gezeigt, dass das Axiom I.0 unabhängig von den Axiomen I.1 bis I.7 ist. Warum?
(e) Beweisen Sie: Wählt man zu unseren Knetekugeln als Modellgeraden Stäbchen eines originalen Mikadospiels derart, dass sich alle Geraden paarweise unterscheiden, so kann man kein Modell für die Inzidenzaxiome des Raumes bauen.

Lösung von User Caro44

a) Skizze Caro44 Skizze.JPG


b) Gründe, warum dieses Modell kein Modell für die Inzidenzaxiome des Raumes ist.

- Alle Geraden sind durch die Punkte miteinander vernetzt und liegen somit nach Axiom I.5 in einer Ebene.

- Bei meiner Skizze sind zwei Punkte immer kollinear zueinander. Es gibt somit immer nur drei paarweise verschiedene Punkte, die nicht kollinear zueinander sind. Nach Axiom I.4 liegen diese alle in einer Ebene.


c) Ergänzungen, damit die Inzidenzaxiome I.1 bis I.7 erfüllt sind.

- Gerade durch die Punkte K und B (Axiom I.1)

- Man benötigt noch einen weiteren Punkt, z.B.: Punkt A (Axiom I.6)

--Caro44 12:05, 27. Nov. 2012 (CET)

Lösung von User ...

Von „http://geometrie.zum.de/index.php?title=Lösung_von_Aufgabe_5.2_S_(WS_12_13)&oldid=19059“