Lösung von Aufgabe 6.1 S (WS 12 13): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (→@Sissy66) |
*m.g.* (Diskussion | Beiträge) (→Die Implikation) |
||
| Zeile 28: | Zeile 28: | ||
=====Die Implikation===== | =====Die Implikation===== | ||
| + | Wir setzen voraus, dass für die Punkte <math>A \not= B \not= C \not=A </math> gilt. | ||
| + | Formulierung der Implikation in der Aufgabe:<br /> | ||
| + | ::<math>\operatorname{Zw}(A,B,C) \Rightarrow </math> weder <math>\operatorname{Zw}(A,C,B)</math> noch <math>\operatorname{Zw}(B,A,C)</math> | ||
Version vom 3. Dezember 2012, 16:03 Uhr
|
Aufgabe 6.1Satz:
Beweisen Sie diesen Satz.
Lösung 6.1 von User Hazel12Bemerkungen Sissy66Ich denke, dass die Voraussetzung ist, dass die 3 Punkte paarweise verschieden sind, also: Vor: A,B,C sind paarweise verschieden Beh: Zw(A,B,C) Ann: Zw(A,B,C) und (oBdA.) Zw(B,A,C) Wenn man doch oBdA. hinschreibt, muss man den zweiten Teil des Beweises nicht mehr machen, oder?--Sissy66 14:23, 2. Dez. 2012 (CET) m.g.@Sissy66Eine Implikation kann mehrere Voraussetzungen haben. Im speziellen Fall wäre eine Voraussetzung, dass die drei Punkte paarweise verschieden sind , was noch...?--*m.g.* 13:29, 3. Dez. 2012 (CET) @HazelDie ImplikationWir setzen voraus, dass für die Punkte Formulierung der Implikation in der Aufgabe:
|
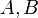 und
und  drei paarweise verschiedene Punkte.
drei paarweise verschiedene Punkte. zwischen den Punkten
zwischen den Punkten  und
und 
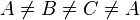 gilt.
gilt.
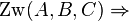 weder
weder 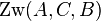 noch
noch