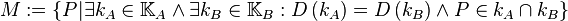Lösung von Aufgabe 7.3 WS 12 13: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „<div style="margin:0; margin-right:4px; border:1px solid #27408B; padding: 1em 1em 1em 1em; background-color:#FFFF99; align:left;"> {|width=90%| style="background…“) |
*m.g.* (Diskussion | Beiträge) |
||
| Zeile 4: | Zeile 4: | ||
<!--- ------------------------------------------------------------------------------------------ ---> | <!--- ------------------------------------------------------------------------------------------ ---> | ||
| + | ==Aufgabe 7.3== | ||
| + | Welcher geometrische Begriff, den Sie aus der Schule kennen, wird im Folgenden beschrieben? Ebene Geometrie sei vorausgesetzt. | ||
| + | Es seien <math>A</math> und <math> B</math> zwei Punkte. Ferner sei <math>\mathbb{K}_A</math> die Menge aller Kreise mit dem Mittelpunkt <math>A</math>. Analog wollen wir unter <math>\mathbb{K}_B</math> die Menge aller Kreise mit dem Mittelpunkt <math>B</math> verstehen. | ||
| + | Auf der Menge <math>\mathbb{K}</math> aller Kreise der Ebene sei die Funktion <math>D: \mathbb{K} \rightarrow \mathbb{R}</math> definiert, die jeden Kreis auf die Länge seiner Durchmesser abbildet. <br /> | ||
| + | <math>M:=\left\{P|\exist k_A \in \mathbb{K}_A \wedge \exist k_B \in \mathbb{K}_B: D\left(k_A\right)=D\left(k_B\right) \wedge P \in k_A \cap k_B \right\}</math> | ||
Version vom 8. Dezember 2012, 18:12 Uhr
Aufgabe 7.3Welcher geometrische Begriff, den Sie aus der Schule kennen, wird im Folgenden beschrieben? Ebene Geometrie sei vorausgesetzt. Es seien
Lösung von User ...Lösung von User ... |
 und
und  zwei Punkte. Ferner sei
zwei Punkte. Ferner sei 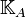 die Menge aller Kreise mit dem Mittelpunkt
die Menge aller Kreise mit dem Mittelpunkt 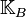 die Menge aller Kreise mit dem Mittelpunkt
die Menge aller Kreise mit dem Mittelpunkt 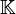 aller Kreise der Ebene sei die Funktion
aller Kreise der Ebene sei die Funktion 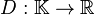 definiert, die jeden Kreis auf die Länge seiner Durchmesser abbildet.
definiert, die jeden Kreis auf die Länge seiner Durchmesser abbildet.