Gruppen, abelsche Gruppen 2012 12: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (→Restklassen modulo 4) |
*m.g.* (Diskussion | Beiträge) (→Restklassen modulo 4) |
||
| Zeile 5: | Zeile 5: | ||
<math>\overline{0}:=\left\{..., -8, -4, 0, 4, 8, ...\right\}</math> (Menge aller durch 4 teilbaren ganzen Zahlen),<br /> | <math>\overline{0}:=\left\{..., -8, -4, 0, 4, 8, ...\right\}</math> (Menge aller durch 4 teilbaren ganzen Zahlen),<br /> | ||
<math>\overline{1}:=\left\{..., -7, -3, 1, 5, 9, ...\right\}</math> (Menge aller ganzen Zahlen, die bei Division durch 4 den Rest 1 lassen),<br /> | <math>\overline{1}:=\left\{..., -7, -3, 1, 5, 9, ...\right\}</math> (Menge aller ganzen Zahlen, die bei Division durch 4 den Rest 1 lassen),<br /> | ||
| − | <math>\overline{2}:=\left\{..., -6, -2, 2, 6, 10, ...\right\}</math> (Menge aller ganzen Zahlen, die bei Division durch 4 den Rest 2 lassen), | + | <math>\overline{2}:=\left\{..., -6, -2, 2, 6, 10, ...\right\}</math> (Menge aller ganzen Zahlen, die bei Division durch 4 den Rest 2 lassen),<br /> |
<math>\overline{3}:=\left\{..., -5, -1, 3, 7, 11, ...\right\}</math> (Menge aller ganzen Zahlen, die bei Division durch 4 den Rest 3 lassen),<br /> | <math>\overline{3}:=\left\{..., -5, -1, 3, 7, 11, ...\right\}</math> (Menge aller ganzen Zahlen, die bei Division durch 4 den Rest 3 lassen),<br /> | ||
Version vom 9. Dezember 2012, 17:29 Uhr
Beispiele für endliche Gruppen
Restklassen modulo 4
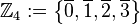
mit
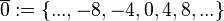(Menge aller durch 4 teilbaren ganzen Zahlen),
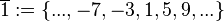(Menge aller ganzen Zahlen, die bei Division durch 4 den Rest 1 lassen),
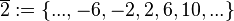(Menge aller ganzen Zahlen, die bei Division durch 4 den Rest 2 lassen),
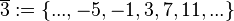(Menge aller ganzen Zahlen, die bei Division durch 4 den Rest 3 lassen),
