Gruppen, abelsche Gruppen 2012 12: Unterschied zwischen den Versionen
Jessy* (Diskussion | Beiträge) (→Gruppe der Deckdrehungen des Quadrats) |
Jessy* (Diskussion | Beiträge) (→Gruppe der Deckabbildungen des Rechtecks) |
||
| Zeile 52: | Zeile 52: | ||
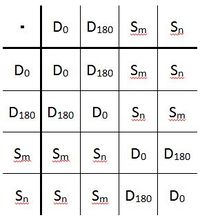
Es ergibt sich folgende Verknüpfungstafel:<br /> | Es ergibt sich folgende Verknüpfungstafel:<br /> | ||
[[Bild:Verknüpfungstafel_DR.4.JPG| 200px]]<br /><br /> | [[Bild:Verknüpfungstafel_DR.4.JPG| 200px]]<br /><br /> | ||
| + | <u>'''Überprüfung der Gruppeneigenschaften:'''</u><br /> | ||
| + | 1. Abgeschlossenheit: siehe Verknüpfungstabelle<br /> | ||
| + | 2. Assoziativität: <br /> | ||
| + | 3. Neutrales Element: <math>D_{0}</math><br /> | ||
| + | 4. Inverse Elemente: <math>D_{0} \cdot D_{0}= D_{0}</math> und <math>D_{180} \cdot D_{180} = D_{0}</math> und <math>S_{m} \cdot S_{m} = D_{0}</math> und <math>S_{n} \cdot S_{n} = D_{0}</math><br /><br /> | ||
Anmerkung: Die Gruppe der Deckabbildungen des Rechtecks ist die kleinste nicht-zyklische Gruppe und wird auch '''Kleinsche Vierergruppe''' genannt. | Anmerkung: Die Gruppe der Deckabbildungen des Rechtecks ist die kleinste nicht-zyklische Gruppe und wird auch '''Kleinsche Vierergruppe''' genannt. | ||
Version vom 12. Dezember 2012, 10:17 Uhr
|
Beispiele für endliche GruppenRestklassen modulo 4
Wir definieren auf Die Struktur
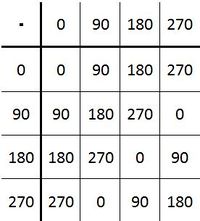
Die folgende Verknüpfungstafel verdeutlicht die obigen Eigenschaften:
Die Tabelle wurde mit der Tabellenkalkulation von Geogebra generiert. Aus diesem Grunde fehlen die Querstriche über den Klassen. Die Verknüpfungstabelle zeigt eine weitere Eigenschaft der Gruppe
Kommutative Gruppen werden auch Abelsche Gruppen genannt. Gruppe der Deckdrehungen des QuadratsHierbei verstehen wir unter Gruppe der Deckabbildungen des Rechtecks
|
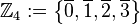
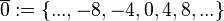 (Menge aller durch 4 teilbaren ganzen Zahlen),
(Menge aller durch 4 teilbaren ganzen Zahlen),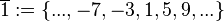 (Menge aller ganzen Zahlen, die bei Division durch 4 den Rest 1 lassen),
(Menge aller ganzen Zahlen, die bei Division durch 4 den Rest 1 lassen),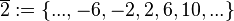 (Menge aller ganzen Zahlen, die bei Division durch 4 den Rest 2 lassen),
(Menge aller ganzen Zahlen, die bei Division durch 4 den Rest 2 lassen),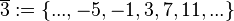 (Menge aller ganzen Zahlen, die bei Division durch 4 den Rest 3 lassen),
(Menge aller ganzen Zahlen, die bei Division durch 4 den Rest 3 lassen), eine Verknüpfung
eine Verknüpfung  wie folgt:
wie folgt: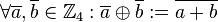
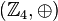 ist eine Gruppe:
ist eine Gruppe:
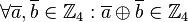 ,
,
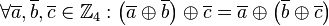 ,
,
 , d.h.
, d.h. 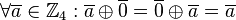 ,
,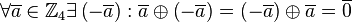 .
.
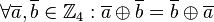 .
.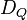 die Menge aller Drehungen die das Quadrat
die Menge aller Drehungen die das Quadrat  auf sich selbst abbilden:
auf sich selbst abbilden: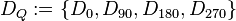
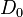
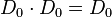 und
und 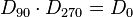 und
und 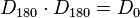 und
und 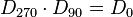
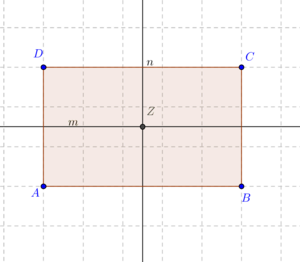
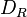 wollen wir die Menge aller Bewegungen verstehen, die das Rechteck
wollen wir die Menge aller Bewegungen verstehen, die das Rechteck  ) und Geradenspiegelungen:
) und Geradenspiegelungen: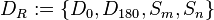
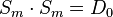 und
und