Lösungen zu den Aufgaben 2: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(Die Seite wurde neu angelegt: „==2.1== ==2.2== Man betrachte den Steigungswinkel <math>\alpha</math> am Steigungsdreieck. Mit der Steigung und dem <math>tan\alpha</math> berechnen Sie den Win…“) |
(→2.2) |
||
| Zeile 14: | Zeile 14: | ||
<math>m=\frac{y_2-y_1}{x_2-x_1}=\frac{-\frac{1}{2}}{-4}=\frac{1}{8}</math><br /> | <math>m=\frac{y_2-y_1}{x_2-x_1}=\frac{-\frac{1}{2}}{-4}=\frac{1}{8}</math><br /> | ||
<math>\tan\alpha=\frac{1}{8} \Rightarrow \alpha = 7,125^\circ </math> | <math>\tan\alpha=\frac{1}{8} \Rightarrow \alpha = 7,125^\circ </math> | ||
| + | |||
| + | ==2.3== | ||
| + | |||
| + | Der Beweis erfolgt durch Einsetzen der Punkte in die Gleichung und Umstellen ;-). | ||
| + | |||
| + | ==2.4== | ||
Version vom 27. Dezember 2012, 11:58 Uhr
Inhaltsverzeichnis |
2.1
2.2
Man betrachte den Steigungswinkel  am Steigungsdreieck. Mit der Steigung und dem
am Steigungsdreieck. Mit der Steigung und dem 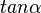 berechnen Sie den Winkel.
berechnen Sie den Winkel.
a) 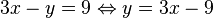 .
.
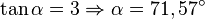
b) 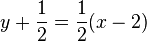
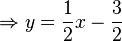
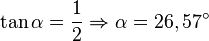
c) 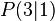 und
und 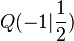
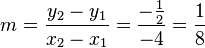
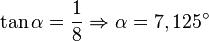
2.3
Der Beweis erfolgt durch Einsetzen der Punkte in die Gleichung und Umstellen ;-).

