Geraden 2012 13: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
K (→Eigenschaften des Normalenvektors) |
(→Der Normalenvektor) |
||
| Zeile 18: | Zeile 18: | ||
<math> E1:\ \ \ \vec{n} \cdot \vec{r} = 0 </math><br><br> | <math> E1:\ \ \ \vec{n} \cdot \vec{r} = 0 </math><br><br> | ||
| − | <math> E2:\ \ \ n =\begin{pmatrix} -r_2 \\ r_1 \end{pmatrix} | + | <math> E2:\ \ \ n =\begin{pmatrix} -r_2 \\ r_1 \end{pmatrix} </math> |
| + | |||
| + | |||
| + | == Hesseform == | ||
| + | (Otto Hesse, deutscher Mathematiker, von 1811-1874)<br> | ||
| + | === Die Punktenormalengleichung === | ||
| + | Eine Möglichkeit ist es Geraden mit Hilfe von zwei Vektoren darzustellen. Hierfür wir zum einen ein Stützvektor, zum anderen ein Richtungsvektor benötigt. | ||
| + | |||
| + | <ggb_applet width="600" height="450" version="4.2" ggbBase64="UEsDBBQACAgIACKOKUIAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAgIACKOKUIAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s3VnbcuS2EX1efwWK5cqTxMGVIDejdUnrcmVTWteWtXG5UnnBkNAMLA5Jk5jRzGbzN/mMvPnH0gDIueli3ZJ1uaQRCLLRQJ/uPt0cjb9ZzUu01G1n6uokIjGOkK7yujDV9CRa2MvjNPrmzVfjqa6netIqdFm3c2VPIh7TaLsOZjFhbrEpYIalEsmEH9OcXB5zgvNjlV4Wx4TRFHOOVZryCKFVZ15X9fdqrrtG5foin+m5Oq9zZb3OmbXN69Ho+vo6HnaP63Y6mk4n8aorIgQnr7qTqL94Der2Fl0zL04xJqOf3p8H9cem6qyqch0hZ9XCvPnq1fjaVEV9ja5NYWeAAU3TCM20mc7AzsxNRk6qAWMbnVuz1B2s3Zl6o+28ibyYqtzzV+EKlRt7IlSYpSl0exLhmAhBZSYwI1iIDGMRobo1urK9MOk3HQ3qxkujr4Ned9XjnElwgunMpNQn0aUqO7DLVJctYAonahcw7ey61BPVDvPtgcgR/ICA+aSdLnBeAOIkohk+okQcSYyPhMDhLLsbR8jWdem1YiQy9PkzophidOQGEgYKQ5KERzjcwywMNAw8DCLI8LCcB1EeZHiQ4eweO/v51tD+xp6lg51s104C9rlPAh8PwIGd6Y6dxBnxGRF3ej8w5M5N/PndwPtpEqbSDwSHgfQPU/fH45U80yL2JIvIzq4hHu7e9Ea8DDsSmmQP35I+y9CNmfQ2M6m4w8xnoruxVOxsCnv5X/+5sSV7lJ13Y/vwHRP+nOR/woYS/z82HI8Gqhv3yYe6mZPt49Xqeedoh2WeeRBBAjIzkUAUApEMBukylCIiEBcwJSlK3CgRc0nJEUMpcnKEIc8vIoU/3CdsggTocjdlyFzEOBIMEc9KHAEXIc9swHKUgYQQSMAitztx27IE8QQmLEUcDug4TTreYLAO5rA5RYwg5tYSiWiCEoqk40XCHV0mqTs7KKUowShxS4EYgRQDIcKKFDFnDUR4U3dmA+5Ml83GKx5HUzULu4ddPi+GS1sfSBd1fnV2gLVWnR2uQQiq0bboheq0VxNfjUs10SW0DhcuDBBaqtJlsNd/WVcWbQgk3Ju2qpmZvLvQ1sKqDv2slupcWb36DqS74YB+a1+rx3qRl6YwqvoRYsSpcArRtnQ7YhpKd8r6bfK6bouLdQeRg1Z/120NFYxmsUy4kCxjmDLmGpJ1/yglMZUUEyoykrEEgO5y5UI+4bCGkEwS7mp3Bhm/vvUR6W3Wy41laqW7Acpp67KpB99N3nVndbm91dSmsm9VYxetb8OAA1tn0mk1LbWH1rMqNDT51aReXQRMWdD1cd3ADIcDTKZv67JuEeQjFdBjTPtxEkYv4062kcJeBnsJPDjJFJvnxBk97cdJGL0UeD0crbeUDGYSPGxjOs8ioHw3xnzIuO5oURl7Pkysya96S0mQ/34xn0C09cv2VZIXUjkeHcTX+Eq3lS5DEFXgyUW96EJYb0Lz1XjR6Q/Kzk6r4gc9hXz8oBwlWlAdRLcnLnRu5rAw3O+hU86tf4OjhruFnrZ6sLD0fW8A1j/FuyF947ZX9V1bz99Vy48QMwdHHY8Ge8Zd3prGhSaaAEdf6W30FaZTwPDF7jowvgMrcsc2AKR1IEZILeysbn1nCzkLvTL666//rirdAktCOLp0LfUcmlpkfVD6uN6459S3y84PqJ78DCSyLcRBYAsbPL81Qn0sq7KZKddT9xiUag0n2EXF63tfF4dYgSu8QUAMTQiKRusQTuHAcNGAOp+EO/724HdoBZkZO3pYuwsBCfEpvEGF1wVnrEvNPRYMdw/8BmEXcPJIz+eqKlDli+q7ykURYBNtCV3hk2h1CqEPppOTaO0vA0wLOwicBb29tt/wxNnTPJGk3hVumIThqa7YAuqWOjyP/cWL4/kjGFe3B2CeBSBPb4C4uB/EZVA2gLS4ieIeHe0E0C6KAy8PnPsCIN6Myq2yDU1bKLxX8G4J9CeGeMfh4i+mKLTvKg65pgv8mavW6g5YMgjAG3VrPzhPIL1qNsG3dcJ9wff2D0ADNMY0JfAunySYMck9+DzmlMuUQ1NAoZ9wnckLxPN9UH77B4AyiZlMkxRnmZRUcBYCmcaCZ5TAI0oZodkLkS1EawsZ4E7cI/RRryyc0Yfxn35Z1PbP/4A0/2f3rzDxCvZdAM3q1gNh+ZflAdOdq4/6p8PWw/ffnW7N5fZ1FAB776N3+2YfDTmOb+R24OcM2uKMSHhdw4JIyXr/EMx5hjOMGbyTM8Z3/fPbkNObkLePgJw+DfIXC/z/KeQixiLFWDJGOYVjyp7aM2CWjCaJFFJyLu4C/AEF8DQUwG9vFMDlowrg8gt7YZePJdklEZEMTUUmMdALhcBNUol5+gWq4+n9HjqHMzzUP+p+/zhzNuir53vnRZqT23ywvt1l4JpjwmJCacp4kmQYimjG7nEVvd9V+pdqz1Fm3pQmN/ZhHMX2OGr6cHZiXxT5lyEhgmOZSPAAT6EmC4Gp9xqJiZAYyjLmOM0ywdLH8T7fw/Trvtair1+jC/vrf+ynpb4Chnk41Pz3X3v770kf74I0xoRLQjhU3xSnIW1kTOBaEJEmPMEZSx6Hv9jHH/WV1zngB5PP7KKado/1gfj9F+Pn+IBikpKUZsBIvK/FSSxSCX0RZRljmUjvrMWj3e9R/Jea/T823/wXUEsHCOFweqPaBwAAiB0AAFBLAQIUABQACAgIACKOKULWN725GQAAABcAAAAWAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYV9qYXZhc2NyaXB0LmpzUEsBAhQAFAAICAgAIo4pQuFweqPaBwAAiB0AAAwAAAAAAAAAAAAAAAAAXQAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAgACAH4AAABxCAAAAAA=" showResetIcon = "false" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /> | ||
Version vom 9. Januar 2013, 17:50 Uhr
Inhaltsverzeichnis |
Der Normalenvektor
Definition des Normalenvektors
Sei g eine Gerade und A ein Punkt auf dieser Geraden. Ein Vektor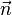 
heisst Normalenvektor von g am Aufpunkt A genau dann, wenn folgendes gilt:
i) 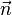steht senkrecht auf der Gerade g
ii)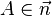 
Skizze eines Normalenvektors
Eigenschaften des Normalenvektors
Sei g eine Gerade mit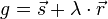 
und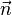 
der Normalenvektor auf g , mit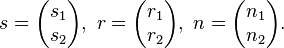 
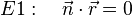
Hesseform
(Otto Hesse, deutscher Mathematiker, von 1811-1874)
Die Punktenormalengleichung
Eine Möglichkeit ist es Geraden mit Hilfe von zwei Vektoren darzustellen. Hierfür wir zum einen ein Stützvektor, zum anderen ein Richtungsvektor benötigt.
