Lösung von Aufg. 10.5 WS 12 13: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) |
|||
| Zeile 1: | Zeile 1: | ||
| − | <div style="margin:0; margin-right:4px; border:1px solid #27408B; padding: 1em 1em 1em 1em; background-color:#FFFF99; align:left;"> | + | --<div style="margin:0; margin-right:4px; border:1px solid #27408B; padding: 1em 1em 1em 1em; background-color:#FFFF99; align:left;"> |
{|width=90%| style="background-color:#FFFF99; padding:1em" | {|width=90%| style="background-color:#FFFF99; padding:1em" | ||
| valign="top" | | | valign="top" | | ||
| Zeile 6: | Zeile 6: | ||
Erläutern Sie, wie und warum sich aus den Satz VII.6 eine neue Möglichkeit, der Definition des Begriffs der Mittelsenkrechte ergibt. | Erläutern Sie, wie und warum sich aus den Satz VII.6 eine neue Möglichkeit, der Definition des Begriffs der Mittelsenkrechte ergibt. | ||
| − | =Lösung von | + | =Lösung von [[Benutzer:Private|Mr. Private ]] 15:10, 19. Jan. 2013 (CET)= |
| + | Sei <math>\overline{AB} </math> eine Strecke. | ||
| + | P und Q sind paarweise verschiedene Punkte. <math>\overline{AP} </math> = <math> \overline{PB}\ \wedge \ \overline{AQ} </math> = <math>\overline{QB} </math>. | ||
| + | Nach Axiom I.1 bildet P, Q eine ''Gerade g''. Die ''Gerade g'' ist die Mittelsenkrechte der Strecke <math>\overline{AB}</math> . | ||
=Lösung von User ...= | =Lösung von User ...= | ||
Version vom 19. Januar 2013, 15:10 Uhr
--
Aufgabe 10.5Erläutern Sie, wie und warum sich aus den Satz VII.6 eine neue Möglichkeit, der Definition des Begriffs der Mittelsenkrechte ergibt. Lösung von Mr. Private 15:10, 19. Jan. 2013 (CET)Sei = Nach Axiom I.1 bildet P, Q eine Gerade g. Die Gerade g ist die Mittelsenkrechte der Strecke Lösung von User ... |
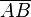eine Strecke.
P und Q sind paarweise verschiedene Punkte.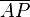 
= Fehler beim Parsen(Lexikalischer Fehler): \overline{PB}\ \wedge \ \overline{AQ}
.
.
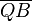