Lösung von Aufgabe 10.2P (WS 12 13): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(Die Seite wurde neu angelegt: „Beweisen Sie mit abbildungsgeometrischen Mitteln den Basiswinkelsatz.<br /> Kategorie:Einführung_P“) |
(table+ table+ table+ table+) |
||
| Zeile 1: | Zeile 1: | ||
Beweisen Sie mit abbildungsgeometrischen Mitteln den Basiswinkelsatz.<br /> | Beweisen Sie mit abbildungsgeometrischen Mitteln den Basiswinkelsatz.<br /> | ||
| + | |||
| + | Voraussetzung: gleichschenkliges Dreieck mit <math>\left| AC \right|</math> = <math>\left| BC \right|</math> | ||
| + | Behauptung: <math>\left| Beta \right|</math> = <math>\left| Alpha \right|</math> | ||
| + | |||
| + | |||
| + | |||
[[Kategorie:Einführung_P]] | [[Kategorie:Einführung_P]] | ||
| + | {| class="wikitable sortable" | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | {| class="wikitable " | ||
| + | ! Schritt | ||
| + | ! Beobachtung | ||
| + | |- | ||
| + | | <math>\left| AC \right|</math> | ||
| + | | Vor. | ||
| + | |- | ||
| + | | m ist Mittelsenkrechte von AB; C <math>\in</math> m | ||
| + | | 1; Mittelsenkrechtenkriterium | ||
| + | |- | ||
| + | | Sm (A) = B | ||
| + | | 2; Def. Geradenspiegelung | ||
| + | |- | ||
| + | | Sm (C) = C | ||
| + | | Def. Fixpunkt | ||
| + | |- | ||
| + | | <math>\left| AM \right|</math> = <math>\left| MB \right|</math> | ||
| + | | Def. Mittelsenkrechte | ||
| + | |- | ||
| + | | Winkel CAM = <math>\alpha</math>; Winkel CBM =<math>\beta</math> | ||
| + | | Def. Winkel | ||
| + | |- | ||
| + | | Sm (<math>\alpha</math>) = <math>\beta</math> | ||
| + | | 5; winkelmaßerhaltung | ||
| + | |} | ||
Version vom 16. Januar 2013, 21:46 Uhr
Beweisen Sie mit abbildungsgeometrischen Mitteln den Basiswinkelsatz.
Voraussetzung: gleichschenkliges Dreieck mit 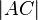 =
= 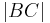 Behauptung:
Behauptung: 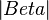 =
= 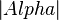
| Schritt | Beobachtung |
|---|---|
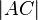
|
Vor. |
m ist Mittelsenkrechte von AB; C  m m
|
1; Mittelsenkrechtenkriterium |
| Sm (A) = B | 2; Def. Geradenspiegelung |
| Sm (C) = C | Def. Fixpunkt |
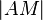 = = 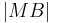
|
Def. Mittelsenkrechte |
Winkel CAM =  ; Winkel CBM = ; Winkel CBM =
|
Def. Winkel |
Sm ( ) = ) = 
|
5; winkelmaßerhaltung |

