Lösung von Zusatzaufgabe 4.1 P (WS 12 13): Unterschied zwischen den Versionen
| Zeile 23: | Zeile 23: | ||
<br /> | <br /> | ||
Mist! Die Seiten müssen jeweils getauscht werden. Die Kontraposition von: <math> A \rightarrow B</math> ist <math> \neg B \rightarrow \neg A</math>.<br /> | Mist! Die Seiten müssen jeweils getauscht werden. Die Kontraposition von: <math> A \rightarrow B</math> ist <math> \neg B \rightarrow \neg A</math>.<br /> | ||
| + | * Genau! Super! Damit wäre die richtig Lösung: | ||
| + | 1.) <math>A \neq B => |AB| \neq 0</math><br /> | ||
| + | 2.) <math>|AB|\neq 0 => A \neq B</math> --[[Benutzer:Tutorin Anne|Tutorin Anne]] 12:23, 20. Jan. 2013 (CET)<br /> | ||
<br /> | <br /> | ||
Annahme1: Der Anstand zweier Punkte A und B ist 0, wenn A und B zwei nicht identische Punkte sind.<br /> | Annahme1: Der Anstand zweier Punkte A und B ist 0, wenn A und B zwei nicht identische Punkte sind.<br /> | ||
Aktuelle Version vom 20. Januar 2013, 12:23 Uhr
Gegeben sei folgende Äquivalenz: Der Abstand zweier Punkte A und B ist genau dann 0, wenn A und B identisch sind.
a) Formulieren Sie die beiden Implikationen, die in dieser Aussage stecken.
b) Wie lautet jeweils die Kontraposition der beiden Implikationen?
c) Wie lauten die beiden Annahmen, wenn Sie diese Implikationen jeweils durch einen Widerspruch beweisen möchten?
A)
Implikation 1: Der Absatnd zweier Punkte A und B ist 0.
Implikation 2: A und B sind identisch.--Hakunamatata 14:50, 26. Nov. 2012 (CET)
Du hast zwar Aussagen formuliert, aber keine Implikationen. Implikationen sind Sätze, bei denen aus einer Aussage A eine weitere (B) folgt. A
B--Tutorin Anne 19:14, 27. Nov. 2012 (CET)
1.) |AB| = 0 => A = B
2.) A = B => |AB| = 0--Unicycle 21:38, 17. Jan. 2013 (CET)
- Top!--Tutorin Anne 19:14, 18. Jan. 2013 (CET)
Kontra 1: Der Abstand zweier Punkte ist größer 0.
Kontra 2: A und B sind verschiedene Punkte. --Hakunamatata 14:50, 26. Nov. 2012 (CET)
Auch Kontrapositionen sind Implikationen. Das muss auch hier geändert werden.--Tutorin Anne 19:14, 27. Nov. 2012 (CET)
1.) 
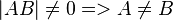
2.) 
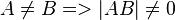--Unicycle 21:38, 17. Jan. 2013 (CET)
- Achtung, hier hat sich ein Fehler eingeschlichen. Was genau ist eine Kontraposition? Was wäre die Kontraposition vom allgemeinen Fall
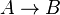?--Tutorin Anne 19:14, 18. Jan. 2013 (CET)
Mist! Die Seiten müssen jeweils getauscht werden. Die Kontraposition von: 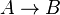ist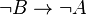 
.
- Genau! Super! Damit wäre die richtig Lösung:
1.)
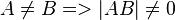
2.) 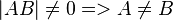--Tutorin Anne 12:23, 20. Jan. 2013 (CET)
Annahme1: Der Anstand zweier Punkte A und B ist 0, wenn A und B zwei nicht identische Punkte sind.
Annahme 2: Der Abstand zweier Punkte ist nicht 0, wenn A und B zwei identische Punkte sind. --Hakunamatata 14:50, 26. Nov. 2012 (CET).
Hier hast du Annahme und Voraussetzung verwoben. Nenne nur die Annahme.--Tutorin Anne 19:14, 27. Nov. 2012 (CET)
1.) 
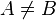
2.) 
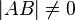--Unicycle 21:38, 17. Jan. 2013 (CET)
- Genau!--Tutorin Anne 19:14, 18. Jan. 2013 (CET)
