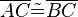Serie 11 (WS 12 13): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (→Was wäre wenn) |
*m.g.* (Diskussion | Beiträge) (→Was wäre wenn nicht) |
||
| Zeile 25: | Zeile 25: | ||
!Nr.!!Beweischritt!!Begründung | !Nr.!!Beweischritt!!Begründung | ||
|- | |- | ||
| − | | (1) || | + | | (1) || <math>m_c</math> schneidet o.B.d.A. <math>\overline{CA}</math> in einem Punkt, den wir <math>c^*</math> nennen wollen || ... |
|- | |- | ||
| (2) || 4 || ... | | (2) || 4 || ... | ||
|} | |} | ||
Version vom 19. Januar 2013, 18:22 Uhr
Inhaltsverzeichnis |
Aufgabe 11.01
Formulieren Sie die Umkehrung des Basiswinkelsatzes.
Aufgabe 11.02
Es seien  drei nicht kollineare Punkte. Die Winkel
drei nicht kollineare Punkte. Die Winkel 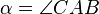 und
und 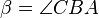 seien kongruent zueinander.
seien kongruent zueinander.
Behauptung:
Ergänzen Sie den folgenden Beweis
(H) Hilfskonstruktion:
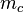 sei die Mittelsenkrechte der Strecke
sei die Mittelsenkrechte der Strecke  .
.
Begründung, dass die Hilfskonstruktion angewendet werden kann:
.................................................
Was wäre wenn
Wenn die Mittelsenkrechte 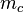 durch
durch  gehen würde, wären die Strecken
gehen würde, wären die Strecken 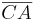 und
und 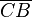 kongruent zueinander.
kongruent zueinander.
Begründung hierfür:
..................................................
Was wäre wenn nicht
Annahme: 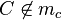
| Nr. | Beweischritt | Begründung |
|---|---|---|
| (1) | 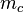 schneidet o.B.d.A. schneidet o.B.d.A. 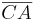 in einem Punkt, den wir in einem Punkt, den wir 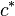 nennen wollen nennen wollen |
... |
| (2) | 4 | ... |