Serie 11 (WS 12 13): Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (→Aufgabe 11.03) |
*m.g.* (Diskussion | Beiträge) (→Aufgabe 11.03) |
||
| Zeile 44: | Zeile 44: | ||
Wegen dieser Identität geht die Mittelsenkrechte <math>m_c</math> durch den Punkt <math>C</math>. Wir haben uns schon überlegt, dass in diesem Fall <math>\overline{AC} \tilde= \overline{BC}</math> gilt. q.e.d. | Wegen dieser Identität geht die Mittelsenkrechte <math>m_c</math> durch den Punkt <math>C</math>. Wir haben uns schon überlegt, dass in diesem Fall <math>\overline{AC} \tilde= \overline{BC}</math> gilt. q.e.d. | ||
=Aufgabe 11.03= | =Aufgabe 11.03= | ||
| − | Es sei <math>\alpha</math> ein Winkel mit den Schenkeln <math>g</math> und <math>h</math> und dem Scheitel <math>S</math>. Ferner sei <math>w</math> die Winkelhalbierende von <math>\alpha</math>, also ein Strahl im Inneren von <math>\alpha</math>, der als Anfangspunkt S hat und <math>\alpha</math> in zwei kongruente Teilwinkel <math>\alpha_1</math> und <math>\alpha_2</math> teilt. Auf <math>w</math> sei ein beliebiger von <math>S</math> verschiedener Punkt <math>P</math> gegeben. | + | Es sei <math>\alpha</math> ein Winkel mit den Schenkeln <math>g</math> und <math>h</math> und dem Scheitel <math>S</math>. Ferner sei <math>w</math> die Winkelhalbierende von <math>\alpha</math>, also ein Strahl im Inneren von <math>\alpha</math>, der als Anfangspunkt S hat und <math>\alpha</math> in zwei kongruente Teilwinkel <math>\alpha_1</math> und <math>\alpha_2</math> teilt. Auf <math>w</math> sei ein beliebiger von <math>S</math> verschiedener Punkt <math>P</math> gegeben. <math>F_g</math> sei der Fußpunkt des Lotes von <math>P</math> auf <math>h</math>. |
Version vom 20. Januar 2013, 16:03 Uhr
Inhaltsverzeichnis |
Aufgabe 11.01
Formulieren Sie die Umkehrung des Basiswinkelsatzes.
Aufgabe 11.02
Es seien  drei nicht kollineare Punkte. Die Winkel
drei nicht kollineare Punkte. Die Winkel 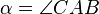 und
und 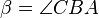 seien kongruent zueinander.
seien kongruent zueinander.
Behauptung:
Ergänzen Sie den folgenden Beweis
(H) Hilfskonstruktion:
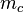 sei die Mittelsenkrechte der Strecke
sei die Mittelsenkrechte der Strecke  .
.
Begründung, dass die Hilfskonstruktion angewendet werden kann:
.................................................
Was wäre wenn
Wenn die Mittelsenkrechte 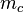 durch
durch  gehen würde, wären die Strecken
gehen würde, wären die Strecken 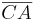 und
und 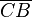 kongruent zueinander.
kongruent zueinander.
Begründung hierfür:
..................................................
Was wäre wenn nicht
Annahme: 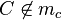
| Nr. | Beweischritt | Begründung |
|---|---|---|
| (1) | 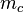 schneidet o.B.d.A. schneidet o.B.d.A. 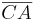 in einem Punkt, den wir in einem Punkt, den wir 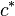 nennen wollen nennen wollen |
... |
| (2) | 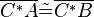 |
... |
| (3) | 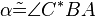 |
... |
| (4) | 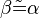 |
... |
| (5) | 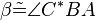 |
... |
Der Rest schreiben wir als kleinen Aufsatz:
Die beiden Winkel  und
und 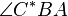 sind also nach der bisherigen Beweisführung kongruent bzw. haben dieselbe Größe.
sind also nach der bisherigen Beweisführung kongruent bzw. haben dieselbe Größe.
Weil sie auch den Schenkel 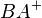 gemeinsam haben und
gemeinsam haben und  und
und 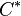 in derselben Halbebene bzgl.
in derselben Halbebene bzgl.  liegen,
liegen,
müssen die die Schenkel 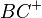 und
und 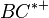 nach dem ... identisch sein.
nach dem ... identisch sein.
Wegen dieser Identität der beiden Strahlen 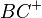 und
und 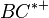 und weil
und weil  der Schnittpunkt von
der Schnittpunkt von 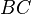 mit
mit 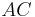 und
und 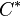 der Schnittpunkt von
der Schnittpunkt von 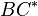 mit
mit 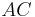 ist, sind ..... identisch.
ist, sind ..... identisch.
Wegen dieser Identität geht die Mittelsenkrechte 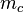 durch den Punkt
durch den Punkt  . Wir haben uns schon überlegt, dass in diesem Fall
. Wir haben uns schon überlegt, dass in diesem Fall 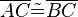 gilt. q.e.d.
gilt. q.e.d.
Aufgabe 11.03
Es sei  ein Winkel mit den Schenkeln
ein Winkel mit den Schenkeln  und
und  und dem Scheitel
und dem Scheitel  . Ferner sei
. Ferner sei  die Winkelhalbierende von
die Winkelhalbierende von  , also ein Strahl im Inneren von
, also ein Strahl im Inneren von  , der als Anfangspunkt S hat und
, der als Anfangspunkt S hat und  in zwei kongruente Teilwinkel
in zwei kongruente Teilwinkel 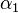 und
und 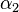 teilt. Auf
teilt. Auf  sei ein beliebiger von
sei ein beliebiger von  verschiedener Punkt
verschiedener Punkt  gegeben.
gegeben. 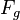 sei der Fußpunkt des Lotes von
sei der Fußpunkt des Lotes von  auf
auf  .
.

