Lösung von Aufgabe 12.02 WS 12 13: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (→Wie zeigen wir das) |
*m.g.* (Diskussion | Beiträge) (→Wie zeigen wir das) |
||
| Zeile 47: | Zeile 47: | ||
# Weil <math>m_b</math> Mittelsenkrechte von <math>b</math> bzw. <math>\overline{AC}</math> ist und <math>M</math> zu <math>m_b</math> gehört, gilt wegen dem Mittelsenkrechtenkriterium: <math>|AM|=|CM|</math> | # Weil <math>m_b</math> Mittelsenkrechte von <math>b</math> bzw. <math>\overline{AC}</math> ist und <math>M</math> zu <math>m_b</math> gehört, gilt wegen dem Mittelsenkrechtenkriterium: <math>|AM|=|CM|</math> | ||
# Nach (1) und (2) ist wegen der Drittengleichheit ist nun <math>|AM|=|BM|</math> und damit <math>M</math> wegen des Mittelsenkrechtenkriteriums ein Punkt der Mittelsenkrechten von <math>c</math>. | # Nach (1) und (2) ist wegen der Drittengleichheit ist nun <math>|AM|=|BM|</math> und damit <math>M</math> wegen des Mittelsenkrechtenkriteriums ein Punkt der Mittelsenkrechten von <math>c</math>. | ||
| + | |||
| + | ===Was bleibt zu zeigen?=== | ||
| + | Wir sollten zeigen dass sich die Mittelsenkrechten in genau einem Punkt schneiden. Es bleibt also zu zeigen, dass <math>M</math> der einzige Punkt aller drei Mittelsenkrechten ist. | ||
| + | |||
| + | ===Wie fast immer, der Highlanderbeweis wird indirekt geführt=== | ||
| + | Annahme: Es existiert ein von <math>M</math> verschiedener Punkt <math>N</math> der zu allen drei Mittelsenkrechten gehört. | ||
| + | |||
| + | Nach der Annahme wären alle unsere Mittelsenkrechten identisch. Warum? ................. | ||
| + | |||
| + | Jetzt ergibt sich folgender Widerspruch: ....... | ||
| + | |||
| + | |||
| + | |||
<!--- Was hier drunter steht muss stehen bleiben ---> | <!--- Was hier drunter steht muss stehen bleiben ---> | ||
|} | |} | ||
Version vom 30. Januar 2013, 16:48 Uhr
Aufgabe 12.02Beweisen Sie: Die Mittelsenkrechten eines Dreiecks schneiden sich in genau einem Punkt.
Lösung User ...
Lösung User Caro44--Caro44 13:16, 30. Jan. 2013 (CET)
Frage HaulerStimmen mit Lösung von Caro44 überein. Frage die aufkam: Wann nimmt man die Definition, wann nimmt man die Existenz und Eindeutigkeit ( in diesem Fall Mittelpunkt, Mittelsenkrechte), wann nimmt das Kriterium als Begründung? Gedanken von uns: Im Beweis benutzen wir Definition nur, wenn Existenz und Eindeutigkeit bewiesen wurde. Kann man sich somit Existenz und Eindeutigkeit sparen und immer Definition schreiben? Weiter folgend kam diese Frage auch bei Definition oder Kriterium Mittelsenkrecht auf. Kriterium setzt sich ja aus beiden Definitionen zusammen! --Hauleri 15:32, 30. Jan. 2013 (CET) Bemerkungen --*m.g.* 16:25, 30. Jan. 2013 (CET)Beide Lösungen sind verbesserungswürdig. Wovon können wir ausgehen?
|
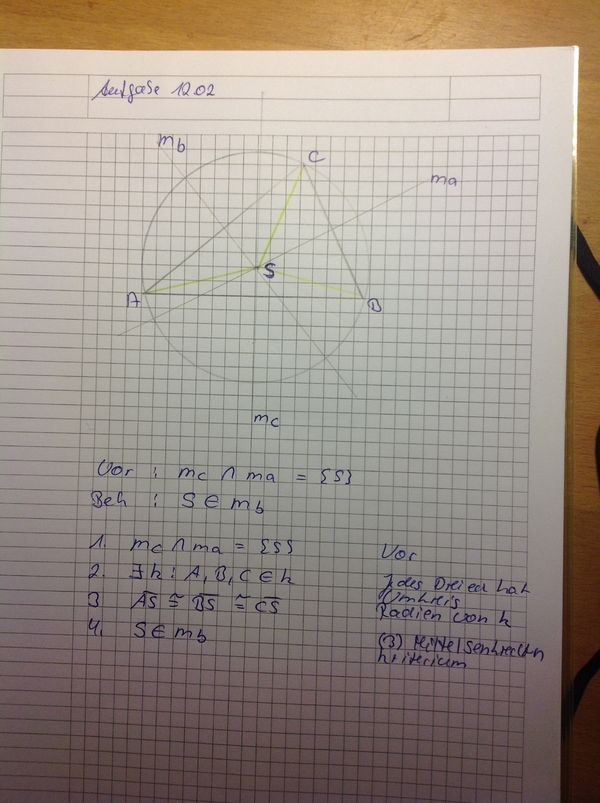

 und irgendwer hat schon gezeigt, dass die Mittelsenkrechten
und irgendwer hat schon gezeigt, dass die Mittelsenkrechten 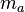 und
und 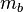 einander im Punkt
einander im Punkt  schneiden. Wir sollen jetzt zeigen, dass auch die dritte Mittelsenkrechte durch eben diesen Punkt geht. Dass jede Strecke genau eine Mittelsenkrechte hat, wissen wir bereits.
schneiden. Wir sollen jetzt zeigen, dass auch die dritte Mittelsenkrechte durch eben diesen Punkt geht. Dass jede Strecke genau eine Mittelsenkrechte hat, wissen wir bereits.
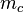 durch
durch  bzw.
bzw.  ist und
ist und 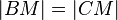
 bzw.
bzw.  ist und
ist und 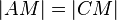
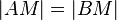 und damit
und damit  .
.
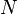 der zu allen drei Mittelsenkrechten gehört.
der zu allen drei Mittelsenkrechten gehört.

