Geraden 2012 13: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(→Die Punktenormalengleichung) |
(→Eigenschaften des Normalenvektors) |
||
| Zeile 19: | Zeile 19: | ||
<math> E1:\ \ \ \vec{n} \cdot \vec{r} = 0 </math><br><br> | <math> E1:\ \ \ \vec{n} \cdot \vec{r} = 0 </math><br><br> | ||
<math> E2:\ \ \ n =\begin{pmatrix} -r_2 \\ r_1 \end{pmatrix} </math> | <math> E2:\ \ \ n =\begin{pmatrix} -r_2 \\ r_1 \end{pmatrix} </math> | ||
| + | <math> E3:\ \ \ Es gibt unendlich viele Normalenvektoren zu einer Gerade g und einem Aufpunkt A </math> | ||
| + | |||
| + | Ist von einer Geraden ein Punkt P und ihr Normalenvektor bekannt, so wird diese hierdurch eindeutig beschrieben. | ||
| + | |||
| + | Es kann zu einem Normalenvektor n und einem Aufpunkt genau eine Gerade gefunden werden, wenn ein weiterer | ||
== Hesseform == | == Hesseform == | ||
Version vom 4. Februar 2013, 17:54 Uhr
Inhaltsverzeichnis |
Der Normalenvektor
Definition des Normalenvektors
Sei g eine Gerade und A ein Punkt auf dieser Geraden. Ein Vektor 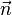 heisst Normalenvektor von g am Aufpunkt A genau dann, wenn folgendes gilt:
heisst Normalenvektor von g am Aufpunkt A genau dann, wenn folgendes gilt:
i) 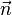 steht senkrecht auf der Gerade g
steht senkrecht auf der Gerade g
ii) 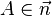
Skizze eines Normalenvektors
Eigenschaften des Normalenvektors
Sei g eine Gerade mit 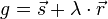 und
und 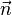 der Normalenvektor auf g , mit
der Normalenvektor auf g , mit 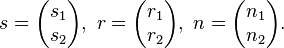
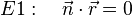
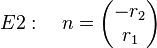
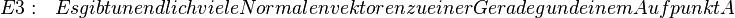
Ist von einer Geraden ein Punkt P und ihr Normalenvektor bekannt, so wird diese hierdurch eindeutig beschrieben.
Es kann zu einem Normalenvektor n und einem Aufpunkt genau eine Gerade gefunden werden, wenn ein weiterer
Hesseform
(Otto Hesse, deutscher Mathematiker, von 1811-1874)
Die Punktenormalengleichung
Eine Möglichkeit ist es Geraden mit Hilfe von zwei Vektoren darzustellen. Hierfür wir zum einen ein Stützvektor, zum anderen ein Richtungsvektor benötigt.

