Geraden 2012 13: Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(→‎Eigenschaften des Normalenvektors)
Zeile 1: Zeile 1:
 +
== Darstellung von Geraden ==
 +
=== Die Punktenormalengleichung ===
 +
Eine Möglichkeit ist es Geraden mit Hilfe von zwei Vektoren darzustellen. Hierfür wir zum einen ein Stützvektor, zum anderen ein Richtungsvektor benötigt.
 +
 +
<ggb_applet width="700" height="450"  version="4.2" ggbBase64="UEsDBBQACAgIACKOKUIAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAgIACKOKUIAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s3VnbcuS2EX1efwWK5cqTxMGVIDejdUnrcmVTWteWtXG5UnnBkNAMLA5Jk5jRzGbzN/mMvPnH0gDIueli3ZJ1uaQRCLLRQJ/uPt0cjb9ZzUu01G1n6uokIjGOkK7yujDV9CRa2MvjNPrmzVfjqa6netIqdFm3c2VPIh7TaLsOZjFhbrEpYIalEsmEH9OcXB5zgvNjlV4Wx4TRFHOOVZryCKFVZ15X9fdqrrtG5foin+m5Oq9zZb3OmbXN69Ho+vo6HnaP63Y6mk4n8aorIgQnr7qTqL94Der2Fl0zL04xJqOf3p8H9cem6qyqch0hZ9XCvPnq1fjaVEV9ja5NYWeAAU3TCM20mc7AzsxNRk6qAWMbnVuz1B2s3Zl6o+28ibyYqtzzV+EKlRt7IlSYpSl0exLhmAhBZSYwI1iIDGMRobo1urK9MOk3HQ3qxkujr4Ned9XjnElwgunMpNQn0aUqO7DLVJctYAonahcw7ey61BPVDvPtgcgR/ICA+aSdLnBeAOIkohk+okQcSYyPhMDhLLsbR8jWdem1YiQy9PkzophidOQGEgYKQ5KERzjcwywMNAw8DCLI8LCcB1EeZHiQ4eweO/v51tD+xp6lg51s104C9rlPAh8PwIGd6Y6dxBnxGRF3ej8w5M5N/PndwPtpEqbSDwSHgfQPU/fH45U80yL2JIvIzq4hHu7e9Ea8DDsSmmQP35I+y9CNmfQ2M6m4w8xnoruxVOxsCnv5X/+5sSV7lJ13Y/vwHRP+nOR/woYS/z82HI8Gqhv3yYe6mZPt49Xqeedoh2WeeRBBAjIzkUAUApEMBukylCIiEBcwJSlK3CgRc0nJEUMpcnKEIc8vIoU/3CdsggTocjdlyFzEOBIMEc9KHAEXIc9swHKUgYQQSMAitztx27IE8QQmLEUcDug4TTreYLAO5rA5RYwg5tYSiWiCEoqk40XCHV0mqTs7KKUowShxS4EYgRQDIcKKFDFnDUR4U3dmA+5Ml83GKx5HUzULu4ddPi+GS1sfSBd1fnV2gLVWnR2uQQiq0bboheq0VxNfjUs10SW0DhcuDBBaqtJlsNd/WVcWbQgk3Ju2qpmZvLvQ1sKqDv2slupcWb36DqS74YB+a1+rx3qRl6YwqvoRYsSpcArRtnQ7YhpKd8r6bfK6bouLdQeRg1Z/120NFYxmsUy4kCxjmDLmGpJ1/yglMZUUEyoykrEEgO5y5UI+4bCGkEwS7mp3Bhm/vvUR6W3Wy41laqW7Acpp67KpB99N3nVndbm91dSmsm9VYxetb8OAA1tn0mk1LbWH1rMqNDT51aReXQRMWdD1cd3ADIcDTKZv67JuEeQjFdBjTPtxEkYv4062kcJeBnsJPDjJFJvnxBk97cdJGL0UeD0crbeUDGYSPGxjOs8ioHw3xnzIuO5oURl7Pkysya96S0mQ/34xn0C09cv2VZIXUjkeHcTX+Eq3lS5DEFXgyUW96EJYb0Lz1XjR6Q/Kzk6r4gc9hXz8oBwlWlAdRLcnLnRu5rAw3O+hU86tf4OjhruFnrZ6sLD0fW8A1j/FuyF947ZX9V1bz99Vy48QMwdHHY8Ge8Zd3prGhSaaAEdf6W30FaZTwPDF7jowvgMrcsc2AKR1IEZILeysbn1nCzkLvTL666//rirdAktCOLp0LfUcmlpkfVD6uN6459S3y84PqJ78DCSyLcRBYAsbPL81Qn0sq7KZKddT9xiUag0n2EXF63tfF4dYgSu8QUAMTQiKRusQTuHAcNGAOp+EO/724HdoBZkZO3pYuwsBCfEpvEGF1wVnrEvNPRYMdw/8BmEXcPJIz+eqKlDli+q7ykURYBNtCV3hk2h1CqEPppOTaO0vA0wLOwicBb29tt/wxNnTPJGk3hVumIThqa7YAuqWOjyP/cWL4/kjGFe3B2CeBSBPb4C4uB/EZVA2gLS4ieIeHe0E0C6KAy8PnPsCIN6Myq2yDU1bKLxX8G4J9CeGeMfh4i+mKLTvKg65pgv8mavW6g5YMgjAG3VrPzhPIL1qNsG3dcJ9wff2D0ADNMY0JfAunySYMck9+DzmlMuUQ1NAoZ9wnckLxPN9UH77B4AyiZlMkxRnmZRUcBYCmcaCZ5TAI0oZodkLkS1EawsZ4E7cI/RRryyc0Yfxn35Z1PbP/4A0/2f3rzDxCvZdAM3q1gNh+ZflAdOdq4/6p8PWw/ffnW7N5fZ1FAB776N3+2YfDTmOb+R24OcM2uKMSHhdw4JIyXr/EMx5hjOMGbyTM8Z3/fPbkNObkLePgJw+DfIXC/z/KeQixiLFWDJGOYVjyp7aM2CWjCaJFFJyLu4C/AEF8DQUwG9vFMDlowrg8gt7YZePJdklEZEMTUUmMdALhcBNUol5+gWq4+n9HjqHMzzUP+p+/zhzNuir53vnRZqT23ywvt1l4JpjwmJCacp4kmQYimjG7nEVvd9V+pdqz1Fm3pQmN/ZhHMX2OGr6cHZiXxT5lyEhgmOZSPAAT6EmC4Gp9xqJiZAYyjLmOM0ywdLH8T7fw/Trvtair1+jC/vrf+ynpb4Chnk41Pz3X3v770kf74I0xoRLQjhU3xSnIW1kTOBaEJEmPMEZSx6Hv9jHH/WV1zngB5PP7KKado/1gfj9F+Pn+IBikpKUZsBIvK/FSSxSCX0RZRljmUjvrMWj3e9R/Jea/T823/wXUEsHCOFweqPaBwAAiB0AAFBLAQIUABQACAgIACKOKULWN725GQAAABcAAAAWAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYV9qYXZhc2NyaXB0LmpzUEsBAhQAFAAICAgAIo4pQuFweqPaBwAAiB0AAAwAAAAAAAAAAAAAAAAAXQAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAgACAH4AAABxCAAAAAA=" showResetIcon = "false" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" />
 +
 
== Der Normalenvektor ==
 
== Der Normalenvektor ==
 
=== Definition des Normalenvektors ===
 
=== Definition des Normalenvektors ===

Version vom 4. Februar 2013, 19:08 Uhr

Inhaltsverzeichnis

Darstellung von Geraden

Die Punktenormalengleichung

Eine Möglichkeit ist es Geraden mit Hilfe von zwei Vektoren darzustellen. Hierfür wir zum einen ein Stützvektor, zum anderen ein Richtungsvektor benötigt.

Der Normalenvektor

Definition des Normalenvektors

Sei g eine Gerade. Ein Vektor 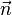\ \vec{n} \ heisst genau dann Normalenvektor von g, wenn 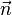\ \vec{n}\ senkrecht zu der Geraden g steht.

Der Punkt A an dem sich ein Normalenvektor mit der Geraden schneidet, wird auch Aufpunkt genannt.



Skizze eines Normalenvektors

Eigenschaften des Normalenvektors

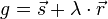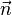Sei g eine Gerade mit \ \ g = \vec{s} + \lambda \cdot \vec{r} \ und \vec{n} der Normalenvektor auf g , mit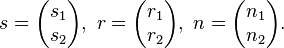 s =\begin{pmatrix} s_1 \\ s_2 \end{pmatrix}, \ r =\begin{pmatrix} r_1 \\ r_2 \end{pmatrix},\ n =\begin{pmatrix} n_1 \\ n_2 \end{pmatrix}.

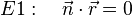
E1:\ \ \ \vec{n} \cdot \vec{r} = 0

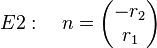
E2:\ \ \ n =\begin{pmatrix} -r_2 \\ r_1 \end{pmatrix}
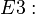E3: Im Raum gibt es unendlich viele Normalenvektoren zu einer Gerade g und einem Aufpunkt A.


Ist in der Ebene von einer Geraden ein Punkt P und ihr Normalenvektor bekannt, so wird diese hierdurch eindeutig beschrieben. Sei 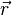\vec{r} ein beliebiger Ortsvektor auf der Geraden g, da der Normalenvektor 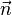\vec{n} senkrecht zu der Geraden 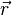\vec{r} steht, so steht 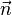\vec{n} auch senkrecht zu jedem anderen Vektor 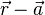\vec{r}- \vec{a} der Geraden g.






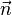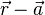Da die beiden Vektoren \vec{n} und \vec{r}-\vec{a} senkrecht zueinander stehen, muss das Skalarprodukt dieser beiden Vektoren Null ergeben:

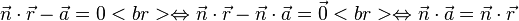
\vec{n} \cdot \vec{r}-\vec{a} = 0 <br> \Leftrightarrow \vec{n} \cdot \vec{r} - \vec{n} \cdot \vec{a} = \vec{0}<br> \Leftrightarrow \vec{n} \cdot \vec{a} = \vec{n} \cdot \vec{r}

(geometrische Deutung)

Hesseform

(Otto Hesse, deutscher Mathematiker, von 1811-1874)

Die Punktenormalengleichung

Eine Möglichkeit ist es Geraden mit Hilfe von zwei Vektoren darzustellen. Hierfür wir zum einen ein Stützvektor, zum anderen ein Richtungsvektor benötigt.

Von „http://geometrie.zum.de/index.php?title=Geraden_2012_13&oldid=21517“