Lösung von Aufg. 6.3P (WS 12/13): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
| Zeile 4: | Zeile 4: | ||
* Im Grundgedanken richtig. Die Formulierung nicht gut und ungeschickt. Du solltest erst die Punkte A und B nennen ...--[[Benutzer:Tutorin Anne|Tutorin Anne]] 13:38, 4. Feb. 2013 (CET) | * Im Grundgedanken richtig. Die Formulierung nicht gut und ungeschickt. Du solltest erst die Punkte A und B nennen ...--[[Benutzer:Tutorin Anne|Tutorin Anne]] 13:38, 4. Feb. 2013 (CET) | ||
| − | Eine Menge von Punkten heißt konvex, wenn für zwei beliebige Punkte A,B gilt:<br /> | + | Eine Menge von Punkten heißt konvex, wenn für zwei beliebige Punkte A,B '''dieser Menge''' gilt:<br /> |
| − | <math>\forall A, B \in M:=</math> <math>\overline{AB}</math> Teilmenge von M--[[Benutzer:Hakunamatata|Hakunamatata]] 19:21, 4. Feb. 2013 (CET)<br /> | + | <math>\forall A, B \in M:=</math> <math>\overline{AB} </math> Teilmenge von M--[[Benutzer:Hakunamatata|Hakunamatata]] 19:21, 4. Feb. 2013 (CET)<br /> |
| + | * Gut. Allerdings ist hier das Defniertzeichen := falsch. Es werden ja nicht alle Punkte definiert als eine Strecke. Hier gehört ein Implikationszeichen <math>\Rightarrow</math> hin.--[[Benutzer:Tutorin Anne|Tutorin Anne]] 16:08, 5. Feb. 2013 (CET) | ||
[[Kategorie:Einführung_P]] | [[Kategorie:Einführung_P]] | ||
Aktuelle Version vom 5. Februar 2013, 16:08 Uhr
Definieren Sie den Begriff: "konvexe Punktmenge".
Eine Menge M heißt konvexe Punktmenge wenn die Menge aller Punkte der Strecke 
Element M sind. Wobei A und B zwei beliebige Punkte von M sind. --Würmli 11:23, 4. Feb. 2013 (CET)
- Im Grundgedanken richtig. Die Formulierung nicht gut und ungeschickt. Du solltest erst die Punkte A und B nennen ...--Tutorin Anne 13:38, 4. Feb. 2013 (CET)
Eine Menge von Punkten heißt konvex, wenn für zwei beliebige Punkte A,B dieser Menge gilt:
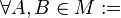
Teilmenge von M--Hakunamatata 19:21, 4. Feb. 2013 (CET)
- Gut. Allerdings ist hier das Defniertzeichen := falsch. Es werden ja nicht alle Punkte definiert als eine Strecke. Hier gehört ein Implikationszeichen
hin.--Tutorin Anne 16:08, 5. Feb. 2013 (CET)
