Lösung von Zusatzaufgabe 12.2P (WS 12 13): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
| Zeile 22: | Zeile 22: | ||
|2. D(mb,180)(A)=C ^ D(mb,180)(B)=B' ||1.), Def. Punktspiegelung, Def. Mittelpunkt | |2. D(mb,180)(A)=C ^ D(mb,180)(B)=B' ||1.), Def. Punktspiegelung, Def. Mittelpunkt | ||
|- | |- | ||
| − | |2.1 <math>B'C \equiv g</math> ||1.),2.) || Warum folgt das aus Schritt 1 und 2? || | + | |2.1 <math>B'C \equiv g</math> ||1.),2.) || Warum folgt das aus Schritt 1 und 2? || Man müsste vllt. noch Satz IX.4 erwähnen, sodass gilt AB parallel C'B und laut Parallelenaxiom gibt es nur eine parallele Gerade durch C, heißt B'C muss auf g zu liegen kommen. |
|- | |- | ||
| − | |3. <math>\alpha \tilde {=}\alpha '</math> || Wechselwinkelsatz, 1.),2.),2.1), Eig. Punktspiegelung (winkeltreue), winkelmaßerhaltend || Das sind zu viele Begründungen, entscheide dich! || ( | + | |3. <math>\alpha \tilde {=}\alpha '</math> || Wechselwinkelsatz, 1.),2.),2.1), Eig. Punktspiegelung (winkeltreue), winkelmaßerhaltend || Das sind zu viele Begründungen, entscheide dich! || Eig. Punktspiegelung (winkeltreue), 2.1),2.) |
|- | |- | ||
|4. D(ma,180)(A)=A' ^D(ma,180)(B)=C || 1.), Def. Punktspiegelung, Def. Mittelpunkt | |4. D(ma,180)(A)=A' ^D(ma,180)(B)=C || 1.), Def. Punktspiegelung, Def. Mittelpunkt | ||
|- | |- | ||
| − | |5. <math>\beta \tilde {=} \beta'</math> || 4.),2.1) Wechselwinkelsatz, Eig. Punktspiegelung (winkeltreue), winkelmaßerhaltend ||Das sind zu viele Begründungen, entscheide dich! || ( | + | |5. <math>\beta \tilde {=} \beta'</math> || 4.),2.1) Wechselwinkelsatz, Eig. Punktspiegelung (winkeltreue), winkelmaßerhaltend ||Das sind zu viele Begründungen, entscheide dich! || Eig. Punktspiegelung (winkeltreue), 2.1),4.) |
|- | |- | ||
| − | |6. <math>\left| \alpha' \right| + \left| \beta' \right|+ \left| \gamma \right|= 180</math> || 4.), 5.),Def. Nebenwinkel, Satz(Nebenwinkel sind supplementär)|| Woher weißt | + | |6. <math>\left| \alpha' \right| + \left| \beta' \right|+ \left| \gamma \right|= 180</math> || 4.), 5.),Def. Nebenwinkel, Satz(Nebenwinkel sind supplementär)|| Woher weißt du, dass sie alle an einer Geraden liegen?|| Die Winkel alpha',beta',gamma' besitzen alle den gleichen Scheitelpunkt, nämlich C. Das ist anzunehmen, da der Winkel alpha mit dem Scheitelpunkt A punktgespiegelt wird und alpha' nun den Scheitelpunkt C hat.(Für B analog). Der Winkel Gamma hat ja schon den Scheitelpunkt C. |
|- | |- | ||
|7. <math>\left| \alpha \right| + \left| \beta \right|+ \left| \gamma \right|= 180</math> || 3.),5.),6.) | |7. <math>\left| \alpha \right| + \left| \beta \right|+ \left| \gamma \right|= 180</math> || 3.),5.),6.) | ||
Version vom 6. Februar 2013, 11:51 Uhr
Beweisen Sie den Innenwinkelsatz für Dreiecke mit Hilfe zweier Punktspiegelungen.
| Voraussetzung | Dreieck ABC mit den Innenwinkeln 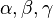
|
| Behauptung | 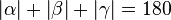
|
| Beweisschritte | Begründung | Hinweis (Tutorin_Anne) | Änderungsvorschläge |
|---|---|---|---|
1. Wir konstruieren eine Gerade g, für die gilt g ll  ^ C ^ C g g |
Parallelenaxiom, Vor. | ||
| 2. D(mb,180)(A)=C ^ D(mb,180)(B)=B' | 1.), Def. Punktspiegelung, Def. Mittelpunkt | ||
2.1 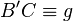 |
1.),2.) | Warum folgt das aus Schritt 1 und 2? | Man müsste vllt. noch Satz IX.4 erwähnen, sodass gilt AB parallel C'B und laut Parallelenaxiom gibt es nur eine parallele Gerade durch C, heißt B'C muss auf g zu liegen kommen. |
3. 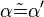 |
Wechselwinkelsatz, 1.),2.),2.1), Eig. Punktspiegelung (winkeltreue), winkelmaßerhaltend | Das sind zu viele Begründungen, entscheide dich! | Eig. Punktspiegelung (winkeltreue), 2.1),2.) |
| 4. D(ma,180)(A)=A' ^D(ma,180)(B)=C | 1.), Def. Punktspiegelung, Def. Mittelpunkt | ||
5. 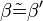 |
4.),2.1) Wechselwinkelsatz, Eig. Punktspiegelung (winkeltreue), winkelmaßerhaltend | Das sind zu viele Begründungen, entscheide dich! | Eig. Punktspiegelung (winkeltreue), 2.1),4.) |
6. 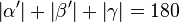 |
4.), 5.),Def. Nebenwinkel, Satz(Nebenwinkel sind supplementär) | Woher weißt du, dass sie alle an einer Geraden liegen? | Die Winkel alpha',beta',gamma' besitzen alle den gleichen Scheitelpunkt, nämlich C. Das ist anzunehmen, da der Winkel alpha mit dem Scheitelpunkt A punktgespiegelt wird und alpha' nun den Scheitelpunkt C hat.(Für B analog). Der Winkel Gamma hat ja schon den Scheitelpunkt C. |
7. 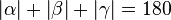 |
3.),5.),6.) |
--TobiWan 00:37, 3. Feb. 2013 (CET)
- Im Großen und Ganzen stimmt der Beweis. Ich habe ein paar Kleinigkeiten angemerkt.--Tutorin Anne 17:49, 5. Feb. 2013 (CET)

