Quiz der Woche 10: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
| Zeile 6: | Zeile 6: | ||
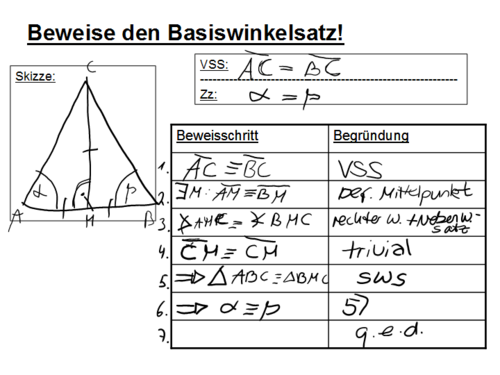
|| Es steht da eigentlich, dass die beiden Seiten <math>\overline{AC}</math> und <math>\overline{BC}</math> identisch sind, es sind ja aber nicht die gleichen Seiten, sondern die Seiten sind kongruent zueinander bzw. die Länge der Seiten sind gleich. | || Es steht da eigentlich, dass die beiden Seiten <math>\overline{AC}</math> und <math>\overline{BC}</math> identisch sind, es sind ja aber nicht die gleichen Seiten, sondern die Seiten sind kongruent zueinander bzw. die Länge der Seiten sind gleich. | ||
- Die Behauptung ist korrekt notiert. | - Die Behauptung ist korrekt notiert. | ||
| − | || Auch hier das gleiche Problem. Richtig wäre: <math>\|alpha|=|beta|</math> | + | || Auch hier das gleiche Problem. Richtig wäre: <math>\|\alpha|=|\beta|</math> |
+ Der erste Beweisschritt und seine Begründung ist korrekt. | + Der erste Beweisschritt und seine Begründung ist korrekt. | ||
|| Ja, prima! | || Ja, prima! | ||
Version vom 24. Juni 2010, 13:16 Uhr
| |
|

