Lösung von Aufgabe 5.01 S SoSe 13: Unterschied zwischen den Versionen
(→Lösung User ...) |
(→Lösung User ...) |
||
| Zeile 19: | Zeile 19: | ||
==Lösung User ...== | ==Lösung User ...== | ||
| − | 1. In Axiom I/1 heißt es „Zu zwei beliebigen verschiedenen Punkten gibt es genau eine Gerade, die mit diesen beiden Punkten inzidiert“. Bei G ist die Gerade G = {C,D} nicht genannt. Entweder C und D sind identisch oder das Modell ist unvollständig. | + | 1. In Axiom I/1 heißt es „Zu zwei beliebigen verschiedenen Punkten gibt es genau eine Gerade, die mit diesen beiden Punkten inzidiert“. Bei G ist die Gerade G = {C,D} nicht genannt. Entweder C und D sind identisch oder das Modell ist unvollständig. Sind C und D identisch, so ist das Modell in der Ebene. |
| − | Was mir noch nicht ganz klar ist: Woher weiß ich, ob die Punkte in der Ebene oder im Raum angeordnet sind? Die Inzidenzaxiome der ebenen Geometrie beziehen sich ja auf drei Punkte, aber | + | Was mir noch nicht ganz klar ist: Woher weiß ich, ob die Punkte in der Ebene oder im Raum angeordnet sind? Die Inzidenzaxiome der ebenen Geometrie beziehen sich ja auf drei Punkte, aber hier sind es ja vier Punkte, sie können also in der Ebene oder im Raum angeordnet werden?!? |
Version vom 29. Mai 2013, 11:29 Uhr
Aufgabe 5.01Wir betrachten das folgende Modell
Lösung User ...1. In Axiom I/1 heißt es „Zu zwei beliebigen verschiedenen Punkten gibt es genau eine Gerade, die mit diesen beiden Punkten inzidiert“. Bei G ist die Gerade G = {C,D} nicht genannt. Entweder C und D sind identisch oder das Modell ist unvollständig. Sind C und D identisch, so ist das Modell in der Ebene.
--Userin24 20:19, 28. Mai 2013 (CEST) Lösung User ...Lösung User ...zurück zu Serie 5 SoSe 2013 |
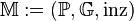 für die Inzidenzgeometrie:
für die Inzidenzgeometrie: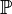 :
: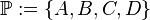
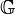 :
: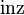 :
: inzidiert mit einer Geraden
inzidiert mit einer Geraden  , wenn er zu
, wenn er zu 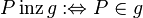
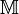 kein Modell für die ebene Inzidenzgeometrie?
kein Modell für die ebene Inzidenzgeometrie?
