Dreieckskongruenz: Unterschied zwischen den Versionen

Version vom 27. Juni 2010, 16:50 Uhr

Wir erinnern uns an die Diskussion zu Anfang des Semesters.

Die Auswertung des Quiz zeigt: Alle drei Aussagen sind synonym.

Momentan jedoch eigentlich noch nicht. Uns fehlt eine Definition des Begriffs der Streckenkongruenz.

Zwei Strecken sind kongruent, wenn sie dieselbe Länge haben.

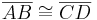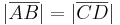
In Zeichen $\overline{AB} \cong \overline{CD}$ := $|\overline{AB}| = |\overline{CD}|$

@@ Zeile 17: / Zeile 17: @@
 Momentan jedoch eigentlich noch nicht. Uns fehlt eine Definition des Begriffs der Streckenkongruenz.
+===== Definition VII.1: (Streckenkongruenz) =====
+:: Zwei Strecken sind kongruent, wenn sie dieselbe Länge haben.<br />
+:: In Zeichen <math>\overline{AB} \cong \overline{CD}</math> := <math>|\overline{AB}| = |\overline{CD}|</math>
 == Winkelkongruenz ==

	Die Strecken $\overline{AB}$ und $\overline{CD}$ sind kongruent zueinander.
	Der Punkt $\ A$ hat zum Punkt $\ B$ denselben Abstand wie der Punkt $\ C$ zum Punkt $\ D$
	Die Strecken $\overline{AB}$ und $\overline{CD}$ haben dieselbe Länge.