Lösung der Aufgaben zur Aussagenlogik (WS 13/14): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(Die Seite wurde neu angelegt: „== Aussagenlogik == Bitte rufen Sie sich die Aussagenlogik ins Gedächtnis. Eine gute Wiederholung (bzw. eine gute Einführung, falls Sie die mathematischen Grun…“) |
(→Aussagenlogik) |
||
| Zeile 6: | Zeile 6: | ||
* (A <math>\Rightarrow</math> B) <math>\Leftrightarrow</math> ( <math>\neg A</math> <math>\vee </math> B) | * (A <math>\Rightarrow</math> B) <math>\Leftrightarrow</math> ( <math>\neg A</math> <math>\vee </math> B) | ||
* <math>\neg (A \wedge B)</math> <math>\Leftrightarrow</math> (<math>\neg A</math> <math>\vee </math> <math>\neg B</math>) | * <math>\neg (A \wedge B)</math> <math>\Leftrightarrow</math> (<math>\neg A</math> <math>\vee </math> <math>\neg B</math>) | ||
| + | |||
| + | Damit es nicht zu schwierig wird, hier schon mal die Tabelle. Die Zahlen sind mit Inhalt zu ersetzen. --[[Benutzer:Tutorin Anne|Tutorin Anne]] 08:46, 29. Okt. 2013 (CET) | ||
| + | |||
| + | |||
| + | {| class="wikitable sortable" | ||
| + | !A!!B!!A <math>\Rightarrow</math> B!!<math>\neg A</math>!!<math>\neg A</math> <math>\vee </math> B | ||
| + | |- | ||
| + | | 1 || 2 || 3 ||4 || 5 | ||
| + | |- | ||
| + | | 11 || 12 || 13 || 14 || 15 | ||
| + | |- | ||
| + | | 21 || 22 || 23 || 24 || 25 | ||
| + | |- | ||
| + | | 31 || 32 || 33 || 34 || 35 | ||
| + | |} | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
[[Kategorie:Einführung_P]] | [[Kategorie:Einführung_P]] | ||
Version vom 29. Oktober 2013, 08:46 Uhr
Aussagenlogik
Bitte rufen Sie sich die Aussagenlogik ins Gedächtnis. Eine gute Wiederholung (bzw. eine gute Einführung, falls Sie die mathematischen Grundlagen 1 noch nicht besucht haben) finden Sie bei youtube. Geben Sie dort "Spannagel Aussagenlogik" ein und sehen Sie sich Teil 1 bis 3 an.
Beweisen Sie mit einer Wahrheitstabelle:
- (A
 B)
B)  (
( 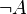
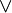 B)
B)
-
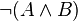
 (
(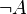
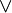
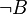 )
)
Damit es nicht zu schwierig wird, hier schon mal die Tabelle. Die Zahlen sind mit Inhalt zu ersetzen. --Tutorin Anne 08:46, 29. Okt. 2013 (CET)
| A | B | A  B B |
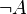 |
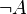 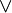 B B
|
|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 |
| 11 | 12 | 13 | 14 | 15 |
| 21 | 22 | 23 | 24 | 25 |
| 31 | 32 | 33 | 34 | 35 |

