Lösung von Aufgabe 3.5 (SoSe 14): Unterschied zwischen den Versionen
| Zeile 12: | Zeile 12: | ||
Aus der Wahrheitstabelle kann man noch kein Schluß ziehen, es fehlt noch ein Schritt und zwar der Widerspruch der zweiten Aussage. <math> - (\ A \wedge \neg B)</math><br /> | Aus der Wahrheitstabelle kann man noch kein Schluß ziehen, es fehlt noch ein Schritt und zwar der Widerspruch der zweiten Aussage. <math> - (\ A \wedge \neg B)</math><br /> | ||
| − | Wenn man das in der Wahrheitstabelle dargestellt hat, merkt man, dass die Implikation und die Negation Äquivalent sind. Es bedeutet für uns, wenn man durch Widerspruch Beweisen möchte, muss man einfach nur die eine Aussage negieren. --[[Benutzer:Picksel|Picksel]] ([[Benutzer Diskussion:Picksel|Diskussion]]) 19:26, 18. Mai 2014 (CEST) | + | Wenn man das in der Wahrheitstabelle dargestellt hat, merkt man, dass die Implikation und die Negation Äquivalent sind. Es bedeutet für uns, wenn man durch Widerspruch Beweisen möchte, muss man einfach nur die eine Aussage negieren. --[[Benutzer:Picksel|Picksel]] ([[Benutzer Diskussion:Picksel|Diskussion]]) 19:26, 18. Mai 2014 (CEST)<br /> |
| + | |||
| + | Ja so ist es. Man kann aber auch an Shamans Wahrheitstabelle erklären, dass wenn man beweisen kann, dass A und nicht B zusammen nicht mögich sind (also ein Widerspurch entsteht), dass dann das Gegenteil gilt und dass ist eben A--> B. --[[Benutzer:Tutorin Anne|Tutorin Anne]] ([[Benutzer Diskussion:Tutorin Anne|Diskussion]]) 19:05, 20. Mai 2014 (CEST)<br /> | ||
| + | |||
[[Category:Einführung_P]] | [[Category:Einführung_P]] | ||
Aktuelle Version vom 20. Mai 2014, 18:05 Uhr
Vergleichen Sie die Wahrheitswerte von
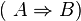 und
und 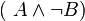 .
.
Erklären Sie den Zusammenhang zwischen Ihrer Wahrheitstabelle und dem indirekten Beweis durch Widerspruch.
Anbei die Wahrheitstabelle. Wie genau ist der indirekte Beweis durch Widerspruch zu führen?
Ist das was aus der Tabelle hervorgeht schon der indirekte Beweis? --Shaman (Diskussion) 18:24, 18. Mai 2014 (CEST)
Aus der Wahrheitstabelle kann man noch kein Schluß ziehen, es fehlt noch ein Schritt und zwar der Widerspruch der zweiten Aussage. 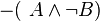
Wenn man das in der Wahrheitstabelle dargestellt hat, merkt man, dass die Implikation und die Negation Äquivalent sind. Es bedeutet für uns, wenn man durch Widerspruch Beweisen möchte, muss man einfach nur die eine Aussage negieren. --Picksel (Diskussion) 19:26, 18. Mai 2014 (CEST)
Ja so ist es. Man kann aber auch an Shamans Wahrheitstabelle erklären, dass wenn man beweisen kann, dass A und nicht B zusammen nicht mögich sind (also ein Widerspurch entsteht), dass dann das Gegenteil gilt und dass ist eben A--> B. --Tutorin Anne (Diskussion) 19:05, 20. Mai 2014 (CEST)


