Übung 08.12.14: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (→Aufgabe III.01) |
*m.g.* (Diskussion | Beiträge) (→Aufgabe III.01) |
||
| Zeile 1: | Zeile 1: | ||
= Aufgabe III.01 = | = Aufgabe III.01 = | ||
Gegeben seien die Gerade <math>l</math> durch die Geradengleichung <math>y(x)=-\frac{1}{4}</math> und der Punkt <math>F \left(0,\frac{1}{4} \right)</math>. Beweisen Sie: Für jeden beliebigen Punkt <math>L</math> auf <math>l</math> gilt: Der Schnittpunkt der Senkrechten <math>s</math> auf <math>l</math> in <math>L</math> mit der Mittelsenkrechten von <math>\overline{FL}</math> ist ein Punkt der Normalparabel. | Gegeben seien die Gerade <math>l</math> durch die Geradengleichung <math>y(x)=-\frac{1}{4}</math> und der Punkt <math>F \left(0,\frac{1}{4} \right)</math>. Beweisen Sie: Für jeden beliebigen Punkt <math>L</math> auf <math>l</math> gilt: Der Schnittpunkt der Senkrechten <math>s</math> auf <math>l</math> in <math>L</math> mit der Mittelsenkrechten von <math>\overline{FL}</math> ist ein Punkt der Normalparabel. | ||
| + | |||
| + | <ggb_applet width="661" height="411" version="4.2" ggbBase64="UEsDBBQACAgIACaJhEUAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAgIACaJhEUAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1szVhtb9s4Ev7c/RUDfU5sUiIpqXC6SPdQXIHsNrj0Fov7Rkm0zY0s6UTZcYr++B2SkvwSpy9JtndIHL4NZzjPDB+OM/t5uypho1qj6+oioBMSgKryutDV4iJYd/PzJPj5zU+zhaoXKmslzOt2JbuLgE3CYLcPRxNB7GZdXARECUGLZH4ehVKeM469NBfqvKAZ53LOlQxpALA1+nVV/yZXyjQyVzf5Uq3kVZ3Lzulcdl3zejq9u7ubDNYndbuYLhbZZGuKAPDklbkI+s5rVHew6S5y4iEhdPrHr1de/bmuTCerXAVgvVrrNz+9mt3pqqjv4E4X3fIiEEkSwFLpxRLd5AwHUyvUoK+Nyju9UQa37g2dz92qCZyYrOz6K9+DcnQngEJvdKFaxGcSpkSksYgZo4kgTMQB1K1WVdcL097odFA322h15/XanjPJSIr7NtrorFQXwVyWBt3S1bxFSPFE7RqHprsvVSbbYbw7ED3DHxTQn5TVhbHzOFwEeLqzkMZnMSFnnBN/ln3DAXR1XTqtBHgKnz9DSEICZ7ahvgmxEcIvET9HIt+EvmG+4V6G+e3MizIvw7wMi77gZz/eOdpPHHg6+Bnt+0nRP/sR+HEAHPmZ7PlJrROfgdrTuyYCe27qzm8b1g+FH8auocQ3tF9M7B+Hl3imR9GTPKJ7Vn0+PG70Qb4MFvFyf7vF8Fl+jl6Gp7wM+SNePhPcwSjle0bRlvt1nwcmo+/y81Fov8OiYM+5+08wGJMfYXA2HZhu1t89MEsr26drp1bGsk6UOuIBChwvpoiRJzjQFJvYXtAQKAfGcUgTELaNIbJ3kkEECVg5GoGjF57gH+buqwCOuuxk7C8uRAx4BNSREgOkInDEhiQXRijBOXDcZK1TazYSwAQOogQYHtBSWmxpI8J9OEbjIUQUIruXxhAKECHElhYps2wpEnt2VBqCICDsVuRF5ETPh7gjgch6gxne1EaP4C5V2YxRcTjqqll3B9jlq2LodvWRdFHnt2+PsFbSdEMfhfAx2r15/nE6eBJfzUqZqRILhxubBgAbWdob7PTP66qDIQVCP7doZbPUublRXYe7DPwpN/JKdmr7DqXNcEBn2r3UM7XOS11oWf2OOWJVWIUwPtyC7h7uKOkt53XdFjf3BhMHtv9RbY1rUTKhKUsEC/EB5owHcO9XwoRMEpKKOIrSNA4TXDG5tAkf0nCSJpQLmrCYxZxgBO4fWePestqMnsmtMgOUi9beph58O3hv3tblbqqpddX9Iptu3boiDDmwtT5dVotSOWgdq2I5k99m9fbGYxp5XR/vGxwRf4Bs8Utd1i3gfQzxULDo28y3TsaebJQiToY4CTIESRfjOk1DJ+HazLdOCqPuj9Z7Sgc3KRnMaONrw+Agx1zK2OJoXenuahh0Or/tPaVe/rf1KsNs67cdqqQvpHI2Pcqv2a1qK1X6LKowkut6bXxaj6n5arY26lp2y8uq+Jda4H28lpYSO1TtRXcnLlSuV7jRz/fQSRvWf+NR/WyhFq0aPCxd1euBdatkP6cfTDtV79p69b7afMScOTrqbDr4MzN5qxubmpAhR9+qXfYV2khk+GJ/Hzpv0Ivcsg0C2VkQA5Drblm3rrDFO4tVIfxDfVIWU6RJygJ7X0u1wqIWOpeVNknG8JSuWrZxgDr7E0nkKHw71HD5kQQFWTZLaevpHoBS3qP1fUictl/r4hgojIPzBmmhsQpsTjRK+Wzq+ksEDSp0d3Av3A57A1tvFu77L02fXFnPj69DhwR3iyW8cXd2VGw7/9RFoRx7e7b4b+W3GJ+latuUOtddn5keyQeYOrIYQXv3bFAdP7wUrCdApd8KqgPTokqHUzhXLdsdPCx+9ugq7OOV16uVrAqoXJ1y7fDavY+S2FT0kKy7YebKK+m3fgX0qyeBTkNPyK59aeBP5vNXoT8nExbjd62UMpGElNKIMxeL878pGB9aZJBFXcnyylLDYVSuEA56Kjjmy8E5YBnzv2SZPWTpmNWeKk5C/WLUoVenqeMQfYv5W20QlLo9jf27B9hn34F99hXs93Lw7wX/C2nNh2hQSgQXLOUsIkmSCPqjo3GjFnb+WwORfzkQptc2YJ3//8SC9xfhREyGUMSCpHEiYsLDOInSp4cCASst4b2vbDmmXAHzsIC7VaqxdfOH6mMrK2P/w3lYuT0etVHxUdyMj1v2IG7X3/OyXD+JvUTiomabzDcvErcw4iFNeRwxSjgXcdzH8eHN8bUQf9ZDcQgLFqA6H90ufiCpf5jPjeocBJH3+FxEJzEby/mnl5ZPYhu9UNXGkbgB2JKhgiJDXTp0tnR8h+jwENG9Fx1P3eotXJJB7HIQuwyHTjR02NDhe6H+1gp2uv99wn257/+9/+YvUEsHCCyWIDf8BgAAjhgAAFBLAQIUABQACAgIACaJhEXWN725GQAAABcAAAAWAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYV9qYXZhc2NyaXB0LmpzUEsBAhQAFAAICAgAJomERSyWIDf8BgAAjhgAAAwAAAAAAAAAAAAAAAAAXQAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAgACAH4AAACTBwAAAAA=" showResetIcon = "false" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /> | ||
Version vom 4. Dezember 2014, 17:09 Uhr
Aufgabe III.01
Gegeben seien die Gerade 
durch die Geradengleichung 
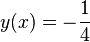und der Punkt 
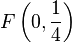. Beweisen Sie: Für jeden beliebigen Punkt 
auf gilt: Der Schnittpunkt der Senkrechten 
auf in mit der Mittelsenkrechten von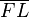 
ist ein Punkt der Normalparabel.
