Benutzer:AlanTu: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
AlanTu (Diskussion | Beiträge) (Kurze Beschreibung) |
AlanTu (Diskussion | Beiträge) (Auftrag der Woche 1 hinzugefügt.) |
||
| Zeile 1: | Zeile 1: | ||
Ich bin Student im ersten Semester, mein Studiengang ist B.A. Sonderpädagogik. | Ich bin Student im ersten Semester, mein Studiengang ist B.A. Sonderpädagogik. | ||
| + | |||
| + | == Auftrag der Woche 1 == | ||
| + | [[Datei:Prismamäppchen.svg|thumb|400px|left]] | ||
| + | Das Mäppchen hat die Form eines Prismas mit trapezförmiger Grundfläche. Die Längen sind <math>h=9\,cm</math>, <math>b_{unten}=5\,cm</math>, <math>b_{oben}=1,5\,cm</math>, <math>l=15,5\,cm</math>. | ||
| + | |||
| + | '''Aus wie viel Stoff (in <math>cm^2</math>, ohne Nahtzugabe) besteht es?''' | ||
| + | |||
| + | <math> | ||
| + | \begin{align} | ||
| + | O_{Stoff} &= O_{Boden} + 2 \cdot (O_{Trapez} + O_{Seitenfl\ddot{a}che}) \\ | ||
| + | &= (l\cdot b_{unten}) + 2 \cdot ((h \cdot \frac{b_{oben} + b_{unten}}{2}) + (l \cdot \sqrt{(\frac{b_{unten}-b_{oben}}{2})^2 + h^2})) \\ | ||
| + | &= (15,5\,cm \cdot 5\,cm) + 2 \cdot ((9\,cm \cdot \frac{1,5\,cm + 5\,cm}{2}) + (15,5\,cm \cdot \sqrt{(\frac{5\,cm-1,5\,cm}{2})^2 + (9\,cm)^2})) \\ | ||
| + | &= 77,5\,cm^2 + 2 \cdot ((9\,cm \cdot 3,25\,cm) + (15,5\,cm \cdot \sqrt{(1,75\,cm)^2 + (9\,cm)^2})) \\ | ||
| + | &= 77,5\,cm^2 + 2 \cdot (29,25\,cm^2 + (15,5\,cm \cdot \sqrt{84,0625}\,cm)) \\ | ||
| + | &\approx 420,23 cm^2 | ||
| + | \end{align} | ||
| + | </math> | ||
Version vom 27. Oktober 2016, 12:31 Uhr
Ich bin Student im ersten Semester, mein Studiengang ist B.A. Sonderpädagogik.
Auftrag der Woche 1
Das Mäppchen hat die Form eines Prismas mit trapezförmiger Grundfläche. Die Längen sind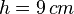 
, 
, 
, 
.
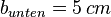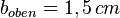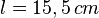Aus wie viel Stoff (in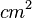 
, ohne Nahtzugabe) besteht es?
