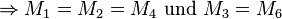Lösung von Aufgabe 1.2 (WS 16 17): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
AlanTu (Diskussion | Beiträge) (Lösung um den Lösungsweg ergänzt.) |
AlanTu (Diskussion | Beiträge) K |
||
| Zeile 54: | Zeile 54: | ||
| − | <math>\Rightarrow M_4 = \{x\vert x\in \mathbb{Q}\wedge x = \pm\sqrt{2}\} = \emptyset</math> (da <math>\sqrt{2}\notin\mathbb{Q}</math>) | + | <math>\Rightarrow M_4 = \{x\vert x\in \mathbb{Q}\wedge x = \pm\sqrt{2}\} = \emptyset</math> (da <math>\pm\sqrt{2}\notin\mathbb{Q}</math>) |
<br><hr><br> | <br><hr><br> | ||
Version vom 24. Oktober 2016, 20:23 Uhr
Geben Sie eine andere Schreibweise der folgenden Mengen an und prüfen Sie, welche Mengen identisch sind.
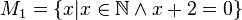
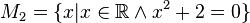
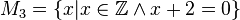
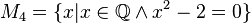
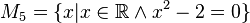
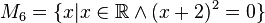
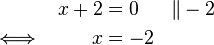
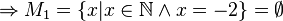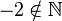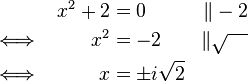
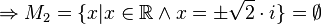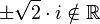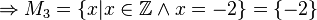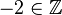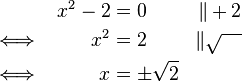
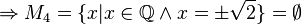(da 
)
(da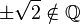 
)
(da 
)
(da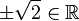 
)
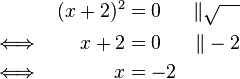
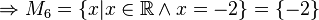(da 
)
(da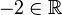 
)
