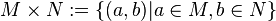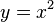Elementare Funktionen: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (→Test) |
*m.g.* (Diskussion | Beiträge) (→Test) |
||
| Zeile 1: | Zeile 1: | ||
=Test= | =Test= | ||
| − | <ggb_applet width="815" height="675" version="4.0" ggbBase64=" | + | <ggb_applet width="815" height="675" version="4.0" ggbBase64="UEsDBBQACAAIADNUUEoAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAAIADNUUEoAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1svVdbb9s2FH5uf8WBnnapbVJ3F3aLtECxAGk3IN0w7GEALdE2G0nURMqWg/74HZKSLCfr0K7FjDi8fTz3C7162ZUFHHijhKzWHp0TD3iVyVxUu7XX6u0s9V6+eLracbnjm4bBVjYl02svNEiR4yQL4yXPsxkh22wWxjSZpVG4nPmbmMR5vMy3YegBdEo8r+Q7VnJVs4zfZnteshuZMW0Z77Wuny8Wx+NxPrCay2a32O02807lHqCYlVp7/eQ5kru4dAws3CeELn5/e+PIz0SlNKsy7oFRoRUvnj5ZHUWVyyMcRa73ay8NqAd7LnZ71CmlvgcLA6rRIDXPtDhwhVcnS6uzLmvPwlhlzp+4GRSjOh7k4iBy3qw9Mqd+sAwTEtEkDNM0ilMPZCN4pXsw7ZkuBnKrg+BHR9fMnJk90FIWG2ZIwseP4BOfwDMzUDf4OMSxOyJujwRu8N0QuiFymNBdDx00dJjQYcLAg4NQYlPwtbdlhUITimrboPvGtdKnglt5+o2z+vQZ6qTEPYIDgnHibI77hDwz3xi/oTlYXCpJJ1x1034h04FlQpLPZ+l/DctgYElJ8JilH31Cy/hfjOtk+Bw1aTSxLLKyf/b7iGPgfwFHt/46hnH4v6i4WgyZsuqTA9TeYHtPal4qky7BEqKliXoKEaZGnGCQR0CXOCQ+YDIAjSCMcElTiM2YQJDgQQgBpGBwNACbG1GK/8LEEoshQmJmN8GUBIqMQogCoDalQsBEApuWmKJ+gIgogggvGfbUNySCGMIYV0EKIcpoMjKhCAzwIq6RvQ8BhcBcpgn4McSGHg1NpsepER1J+hATiKkhiEmNCe2SGfEpBEabuDeXqOpWX5goK/NhqmU9+gLRWI7OVc+Vp4ui+GRVsA0vsE/cGk8CHFhhMsIy2spKw+BE3+3tGlbvRaZuudZ4S8EHdmA3TPPuDaLVwNtiM1mpXxqpX8uiLSsFkMmCjDLLgk7m/ig1LoLJQTg9iCYH8WSe/CNfiSfQKo78ZaMGOMvza4M4lwa05M9VcXrVcHZXS3GpxmphW86Kt1khcsGq3zBYDRdjFxg6kK1WQweKo2QQRDb57UlhBEP3B28kmjaO52TywYpzcic0TOfL6QezT2XM5F5ELu4QLASnTxz1ruOH0UGs46Puu8bkda+3WVyrV7I4b1ntX7Nat419OqB0jdHpqtoV3EaIrbXYl7O7jexuXWgEjtb7U40r4gTY7KzVASuDH0UI6MeNGy3GSDaiiMUQiyBDrIl8PKdL3yLsuHGjRWHwOtF6TemgJiUDG6FsPSPeRdbYyDddvq2EvhkWWmR3vabU4d+15YaP8XNJkn4jkqvFg/ha3fGm4kUfzujJVrbKZeck0nOeiRKX7qA3CDPO+hUFcLs53zV8kLuwjzJnLntKppH6aNuSetPI8ro6vMdIeCDAajFIuVJZI2oTcLDBFnDHzzGVC8Wwg+TTeyb/UPXMdAo0jzamwcxs9V6iq99zpfEeFhXcNalX8BIfWqBtgFVtyRuRjcZm9hGHgrW97P6cOumNpUFuPmC1e+CgiQnx/BMxCKyo98y+/fpIYyfeXNjHknsr857zwLcwj0YoBXbBGcZ8yTpMVKS3UVgJNT6b0SHV+dnsROsrCb45zKO8M48uMzm5HPdgK7qJVdFQ4h4Dw7A9x+U5FzQW6Tt8iCqbsLpPTTv5SeQ5r0ZpWYUhZB2Bdap26gK2CO7Ce7xao/q2KEzc33vG+KirG+RmyPQ2Rg/h5to7wRoY/ADdn9/538OP2I1xDjNIBtoYDMadi0ee7g9Get/Up+QzfUr+u2WxHfDqgJJi98HfTsSxhRPpf6LdD5MOO+HMzk60B91Td2YJoX8a0cEV4mcmuuFqgF1h30zsJBh2Qgsys8hs9bWW/1U58ZUrROiaQmRCP/TjYpqatvv1P+Re/A1QSwcInQ2S/6gFAABlDgAAUEsBAhQAFAAIAAgAM1RQStY3vbkZAAAAFwAAABYAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhX2phdmFzY3JpcHQuanNQSwECFAAUAAgACAAzVFBKnQ2S/6gFAABlDgAADAAAAAAAAAAAAAAAAABdAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAACAAIAfgAAAD8GAAAAAA==" framePossible = "false" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "false" allowRescaling = "true" /> |
=Der Funktionsbegriff= | =Der Funktionsbegriff= | ||
Version vom 16. Februar 2017, 10:34 Uhr
Inhaltsverzeichnis |
Test
Der Funktionsbegriff
Elemente der Mengenlehre
Kreuzprodukt zweier Mengen
Es seien M und N zwei nicht leere Mengen.
Unter dem Kreuzprodukt MxN versteht man die mnge aller geordenten Paare (a,b) mit a aus M und b aus N.