Lösung von Aufgabe 3.09 SoSe 2017 S: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „<div style="margin:0; margin-right:4px; border:1px solid #27408B; padding: 1em 1em 1em 1em; background-color:#FFFF99; align:left;"> {|width=80%| style="backgro…“) |
*m.g.* (Diskussion | Beiträge) |
||
| Zeile 3: | Zeile 3: | ||
| valign="top" | | | valign="top" | | ||
<!--- ---------------------------------------------------------------- ---> | <!--- ---------------------------------------------------------------- ---> | ||
| + | ==Aufgabe 3.09 SoSe 2017 S== | ||
| + | Unter der Umkehrung einer Implikation <math>a \Rightarrow b</math> versteht man die Implikation <math>b \Rightarrow a</math> (Voraussetzung und Behauptung werden getauscht). | ||
| + | # Formulieren Sie die Umkehrung des Satzes von Pythagoras | ||
| + | # Entscheiden Sie (ohne Beweis), ob die Umkehrung des Satzes von Pythagoras eine wahre Aussage ist. | ||
| + | # Oberstudienrätin Schultze-Kröttendörfer läßt ihre 9a die Seiten von Dreiecken vermessen, Quadrate der gemessenen Dreieckseiten bilden, diese Quadrate in geeigneter Weise addieren und vergleichen. Aus diesen Vergleichen sollen die Schüler explizit entscheiden, ob die untersuchten Dreiecke rechtwinklig sind oder nicht. Wenden die Schüler zu dieser Entscheidung den Satz des Pythagoras oder seine Umkehrung an? Begründen Sie Ihre Entscheidung. | ||
| + | ==Lösung 1== | ||
| + | ==Lösung 2== | ||
<!--- ------------------------------------------------------------- ---> | <!--- ------------------------------------------------------------- ---> | ||
Version vom 7. Mai 2017, 10:33 Uhr
Aufgabe 3.09 SoSe 2017 SUnter der Umkehrung einer Implikation
Lösung 1Lösung 2 |
versteht man die Implikation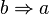 
(Voraussetzung und Behauptung werden getauscht).
