Implikationen SoSe 2017: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) |
*m.g.* (Diskussion | Beiträge) (→Primzahlen) |
||
| Zeile 13: | Zeile 13: | ||
| Die Zahl <math>3</math> ist eine Primzahl.|| wahr | | Die Zahl <math>3</math> ist eine Primzahl.|| wahr | ||
|- | |- | ||
| − | | Die Zahl 4 ist eine Primzahl.|| falsch | + | | Die Zahl <math>4</math> ist eine Primzahl.|| falsch |
|- | |- | ||
| Es gibt unendlich viele Primzahlen.|| wahr | | Es gibt unendlich viele Primzahlen.|| wahr | ||
| Zeile 20: | Zeile 20: | ||
|} | |} | ||
Keine Aussage zu Primzahlen ist:<br /> | Keine Aussage zu Primzahlen ist:<br /> | ||
| − | : Jede natürlich Zahl, die nur durch sich selbst und durch 1 teilbar ist, heißt Primzahl. | + | : Jede natürlich Zahl, die nur durch sich selbst und durch 1 teilbar ist, heißt Primzahl. |
| + | |||
===Wichtige Sätze der Schulgeometrie=== | ===Wichtige Sätze der Schulgeometrie=== | ||
Sätze sind Aussagen, die wahr sind. Eine Aussage, die nicht wahr ist, kann demzufolge auch kein Satz sein. | Sätze sind Aussagen, die wahr sind. Eine Aussage, die nicht wahr ist, kann demzufolge auch kein Satz sein. | ||
Version vom 7. Mai 2017, 13:05 Uhr
Mathematische AussagenBeispielePrimzahlenEs lassen sich z.B. die folgenden Aussagen zu Primzahlen machen:
Keine Aussage zu Primzahlen ist:
Wichtige Sätze der SchulgeometrieSätze sind Aussagen, die wahr sind. Eine Aussage, die nicht wahr ist, kann demzufolge auch kein Satz sein.
|
 ist eine Primzahl.
ist eine Primzahl.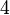 ist eine Primzahl.
ist eine Primzahl.
