|
|
| Zeile 91: |
Zeile 91: |
| | | falsch|| wahr | | | falsch|| wahr |
| | |} | | |} |
| − | | + | Hinweis: Die LaTex-Syntax für das Zeichen <math>\neg</math> ist \neg. |
| | </div> | | </div> |
| | [[Kategorie:Einführung_S]] | | [[Kategorie:Einführung_S]] |
Version vom 7. Mai 2017, 13:43 Uhr
Mathematische Aussagen
Beispiele
Primzahlen
Es lassen sich z.B. die folgenden Aussagen zu Primzahlen machen:
| Aussage |
Wahrheitswert
|
Die Zahl  ist eine Primzahl. ist eine Primzahl. |
wahr
|
Die Zahl 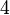 ist eine Primzahl. ist eine Primzahl. |
falsch
|
| Es gibt unendlich viele Primzahlen. |
wahr
|
| Es gibt genauso viele Primzahlen wie es natürliche Zahlen gibt. |
wahr.
|
Keine Aussage zu Primzahlen ist:
- Jede natürlich Zahl, die nur durch sich selbst und durch 1 teilbar ist, heißt Primzahl.
Wichtige Sätze der Schulgeometrie
Sätze sind Aussagen, die wahr sind. Eine Aussage, die nicht wahr ist, kann demzufolge auch kein Satz sein.
- Innenwinkelsatz für Dreiecke: Die Innenwinkelsumme eines jeden Dreiecks ist gleich der Größe eines gestreckten Winkels.
- Satz des Pythagoras: In rechtwinkligen Dreiecken ist die Summe der Quadrate der Katheten gleich dem Quadrat der Hypotenuse.
- Starker Außenwinkelsatz: Jeder Außenwinkel eines Dreiecks ist so groß wie die Summe der beiden nichtanliegenden Innenwinkel des Dreiecks.
- Basiswinkelsatz: Wenn ein Dreieck gleichschenklig ist, dann sind seine Basiswinkel kongruent zueinander.
Ergänzen Sie durch eigene Sätze, die Sie noch aus der Schule kennen:
Begriff der Aussage
Ein sauber Definition des Begriffs mathematische Aussage bleibt uns hier versagt, es reichen intuitive Vorstellungen der folgenden Art:
- Eine Aussage ist ein sprachliches Gebilde, welche zur Beschreibung und Mitteilung von Sachverhalten dienen. (Kleine Enzyklopädie Mathematik. VEB Bibliographisches Institut Leipzig)(1983).
Bei einer mathematischen Aussage setzt man zwei Prinzipien voraus:
- Das Prinzip vom ausgeschlossenen Dritten: Eine Aussage ist wahr (1) oder falsch (0).
- Das Prinzip vom ausgeschlossenen Widerspruch: Eine Aussage kann nicht gleichzeitig wahr und falsch sein.
Beide Prinzipien zusammengefasst:
- Eine mathematische Aussage ist entweder wahr oder falsch.
Weitere Beispiele und Gegenbeispiele für Aussagen
Ergänzen Sie die folgende Tabelle:
| keine Aussage |
Aussage
|
| Gründonnerstag |
Gründonnerstag regnet es immer.
|
| Ab jetzt heißt Raider Twix. |
Im Januar hat man festgelegt, dass Raider Twix heißt.
|
| Die Quadratwurzel aus einer negativen Zahl ziehen. |
Die Quadratwurzel aus einer nagativen Zahl in in  nicht definiert. nicht definiert.
|
| Konstruiere einen Kreis. |
ihr Beispiel
|
| ihr Beispiel |
ihr Beispiel
|
Die Negation einer Aussage
Beispiele
| Aussage |
Negation der Aussage
|
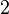 ist Primzahl ist Primzahl |
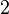 ist keine Primzahl ist keine Primzahl
|
| Die Eisernen steigen auf. |
Die Eisernen steigen nicht auf.
|
| Die Hose ist grün. |
Die Hose ist nicht grün.
|
| ihr Beispiel |
ihr Beispiel
|
| ihr Beispiel |
ihr Beispiel
|
|
Wahrheitswerttabelle
Wenn  eine Aussage ist, dann ist es üblich, mit
eine Aussage ist, dann ist es üblich, mit 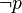 die Negation von
die Negation von  zu kennzeichnen.
zu kennzeichnen.
 |
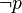
|
| wahr |
falsch
|
| falsch |
wahr
|
Hinweis: Die LaTex-Syntax für das Zeichen  ist \neg.
ist \neg.
 eine Aussage ist, dann ist es üblich, mit
eine Aussage ist, dann ist es üblich, mit 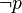 die Negation von
die Negation von  zu kennzeichnen.
zu kennzeichnen.

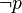
 ist \neg.
ist \neg.
 ist eine Primzahl.
ist eine Primzahl.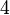 ist eine Primzahl.
ist eine Primzahl. nicht definiert.
nicht definiert.
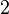 ist Primzahl
ist Primzahl
