Implikationen SoSe 2017: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) |
*m.g.* (Diskussion | Beiträge) (→Implikationen) |
||
| Zeile 4: | Zeile 4: | ||
=Implikationen= | =Implikationen= | ||
| + | ==Generelle Kennzeichnung von Implikationen== | ||
Implikationen sind spezielle mathematische Aussagen, deren Typ sich kurz als wie folgt darstellen bzw. beschreiben lässt: | Implikationen sind spezielle mathematische Aussagen, deren Typ sich kurz als wie folgt darstellen bzw. beschreiben lässt: | ||
* Wenn <math>a</math> dann <math>b</math>. | * Wenn <math>a</math> dann <math>b</math>. | ||
| Zeile 9: | Zeile 10: | ||
* <math>a</math> impliziert <math>b</math>. | * <math>a</math> impliziert <math>b</math>. | ||
* <math>b</math> ist eine Folgerung aus <math>a</math>. | * <math>b</math> ist eine Folgerung aus <math>a</math>. | ||
| + | * Unter der Voraussetzung, dass <math>a</math> gilt, gilt auch <math>b</math>. | ||
| + | * <math>a</math> ist hinreichend dafür, dass <math>b</math> gilt. | ||
* <math>a \Rightarrow b</math> | * <math>a \Rightarrow b</math> | ||
| + | |||
| + | Die Aussage <math>a</math> heißt in der Implikation <math>a \Rightarrow b</math> Voraussetzung, die Aussage <math>b</math> wird Behauptung genannt. | ||
==Beispiele== | ==Beispiele== | ||
===Teilbarkeit durch 3=== | ===Teilbarkeit durch 3=== | ||
Version vom 10. Mai 2017, 15:33 Uhr
ImplikationenGenerelle Kennzeichnung von ImplikationenImplikationen sind spezielle mathematische Aussagen, deren Typ sich kurz als wie folgt darstellen bzw. beschreiben lässt:
Die Aussage BeispieleTeilbarkeit durch 3
|
 dann
dann  .
.

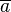 einer natürlichen Zahl
einer natürlichen Zahl  teilbar ist, dann ist auch die Zahl
teilbar ist, dann ist auch die Zahl