Lösung von Aufgabe 4.05 S SoSe 17: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) |
(→Lösung 1) |
||
| Zeile 8: | Zeile 8: | ||
Beweisen Sie <math>A \cap B = A</math>.<br /> | Beweisen Sie <math>A \cap B = A</math>.<br /> | ||
==Lösung 1== | ==Lösung 1== | ||
| + | <math>\frac{36,3}{48,4}x_p - 0,875</math> = <math>\frac{3}{4}x_p - \frac{7}{8}</math> <br/> | ||
| + | <br/> | ||
| + | Da der erste Term gekürzt (mit 12,1) und die Dezimalzahl als Bruch geschrieben, identisch ist mit dem zweiten Term ist <math>A=B</math>. <br/> | ||
| + | |||
| + | Wenn <math>A=B</math> dann ist die Schnittmenge <math>A</math>. Somit gilt <math>A \cap B = A</math>. | ||
| + | |||
==Lösung 2== | ==Lösung 2== | ||
</div> | </div> | ||
[[Category:Einführung_S]] | [[Category:Einführung_S]] | ||
Aktuelle Version vom 18. Mai 2017, 15:48 Uhr
Aufgabe 4.05Wir gehen davon aus, dass wir der ebenen Geometrie ein kartesisches Koordinatensystem zugrunde gelegt haben. Bezüglich dieses Systems definieren wir die folgenden beiden Punktmengen: Beweisen Sie Lösung 1
Wenn Lösung 2 |
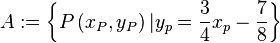
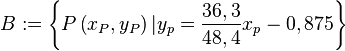
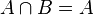 .
.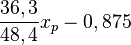 =
= 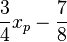
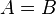 .
.  . Somit gilt
. Somit gilt 
