Lösung von Aufgabe 12.2: Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(→‎Lösung 1)
Zeile 1: Zeile 1:
 
== Aufgabenstellung ==
 
== Aufgabenstellung ==
 
Beweisen Sie:<br />
 
Beweisen Sie:<br />
−
<u>Korollar 1 zum schwachen Außenwinkelsatz</u><br />
+
<u>[[Der_schwache_Außenwinkelsatz| Korollar 1 zum schwachen Außenwinkelsatz]]</u><br />
 
::In jedem Dreieck sind mindestens zwei Innenwinkel spitze Winkel.
 
::In jedem Dreieck sind mindestens zwei Innenwinkel spitze Winkel.
  
Zeile 8: Zeile 8:
 
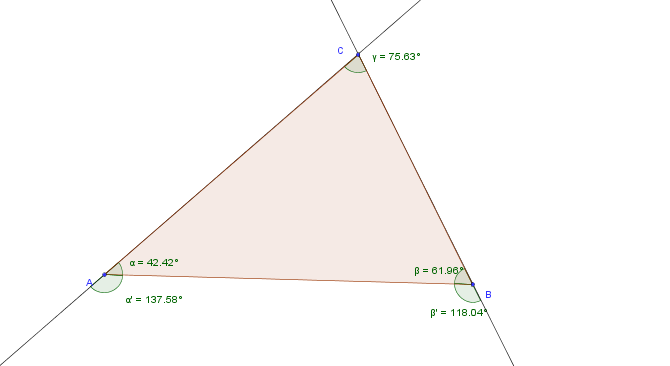
<br />Voraussetzung: Dreieck <math>\overline {ABC}</math>
 
<br />Voraussetzung: Dreieck <math>\overline {ABC}</math>
 
<br />Behauptung: o.B.d.A: <math>|\angle BAC| < 90</math> und <math>|\angle ABC| < 90</math>
 
<br />Behauptung: o.B.d.A: <math>|\angle BAC| < 90</math> und <math>|\angle ABC| < 90</math>
−
<br />Der Einfachheit halber werden die Winkel mit <math>\alpha \beta \gamma</math> bezeichnet, die jeweiligen Außenwinkel sind dann <math>\alpha' \beta' \gamma'</math>
+
<br />Der Einfachheit halber werden die Winkel mit <math>\alpha \ \beta \ \gamma</math> bezeichnet, die jeweiligen Außenwinkel sind dann <math>\alpha' \ \beta' \ \gamma'</math>
 +
<br />Behauptung:
 +
::(1) <math>|\alpha| \ < 90</math> und <math>|\beta| \ < 90</math>
 +
::oder (2) <math>|\alpha| \ < 90</math> und <math>|\gamma| \ < 90</math>
 +
::oder (3) <math>|\beta| \ < 90</math> und <math>|\gamma| \ < 90</math>
 +
<br />[[Bild:Skizze_Übung_12_2.png]]
 
{| class="wikitable "
 
{| class="wikitable "
 
! Nr.
 
! Nr.

Version vom 12. Juli 2010, 01:38 Uhr

Aufgabenstellung

Beweisen Sie:
Korollar 1 zum schwachen Außenwinkelsatz

In jedem Dreieck sind mindestens zwei Innenwinkel spitze Winkel.

Lösung 1

Definition spitzer Winkel: Ein spitzer Winkel ist kleiner als ein rechter Winkel. Definition korrekt? (Diskussion)
Voraussetzung: Dreieck \overline {ABC}
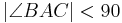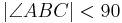
Behauptung: o.B.d.A: |\angle BAC| < 90 und |\angle ABC| < 90
Der Einfachheit halber werden die Winkel mit 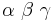\alpha \ \beta \ \gamma bezeichnet, die jeweiligen Außenwinkel sind dann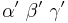 \alpha' \ \beta' \ \gamma'
Behauptung:

(1) |\alpha| \ < 90 und |\beta| \ < 90
oder (2) |\alpha| \ < 90 und |\gamma| \ < 90
oder (3) |\beta| \ < 90 und |\gamma| \ < 90


Skizze Übung 12 2.png

Nr. Beweisschritt Begründung
(I)
(II)
(III)
(IV)
(VI)
(VII)
(VIII)
(IX)
(X)

--Heinzvaneugen 21:48, 11. Jul. 2010 (UTC)

Von „http://geometrie.zum.de/index.php?title=Lösung_von_Aufgabe_12.2&oldid=2976“