Lösung von Aufgabe 1.3 (SoSe 17): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
| Zeile 6: | Zeile 6: | ||
[[Kategorie:Geo_P]] | [[Kategorie:Geo_P]] | ||
M1 c M2 und M1 c M3 (da nicht alle Winkel und Seiten gleich sind) | M1 c M2 und M1 c M3 (da nicht alle Winkel und Seiten gleich sind) | ||
| − | M3 = | + | M3 = M2 (da wenn alle Winkel gleich sind auch alle Seiten automatisch gleich sind) |
| + | |||
| + | Hallo Kissa052,<br/> | ||
| + | deine Aussagen bezüglich den Winkel und Seiten der Dreiecke ist richtig ;) <br/> | ||
| + | Du hast nur das Teilmengenzeichen falsch herum gesetzt. | ||
| + | <math> M_2 \subset M_1 </math> (sprich: Menge <math> M_2 </math> ist eine (echte) Teilmenge von Menge <math> M_1 </math> , | ||
| + | also es gibt weniger gleichseitige, als gleichschenklige Dreiecke, jedoch ist jedes gleichseitige Dreieck auch gleichschenklig, aber nicht umgekehrt) | ||
| + | sowie <math> M_3 \subset M_1 </math>. | ||
| + | Deine Aussage <math> M_3=M_2 </math> stimmt. Setzen wir alles Zusammen erhalten wir: <math> M_2 = M_3 \subset M_1 </math>.<br><br/> | ||
| + | --[[Benutzer:Tutor: Alex|Tutor: Alex]] ([[Benutzer Diskussion:Tutor: Alex|Diskussion]]) 17:34, 31. Mai 2017 (CEST) | ||
Version vom 31. Mai 2017, 16:34 Uhr
Prüfen Sie, welche der folgenden Mengen identisch sind und welche Teilmengenbeziehungen bestehen. Stellen Sie die Teilmengenbeziehungen in einem Venn.Diagramm dar.
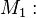Menge aller gleichschenkligen Dreiecke
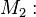Menge aller gleichseitigen Dreiecke
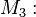Menge aller gleichwinkligen Dreiecke
M1 c M2 und M1 c M3 (da nicht alle Winkel und Seiten gleich sind)
M3 = M2 (da wenn alle Winkel gleich sind auch alle Seiten automatisch gleich sind)
Hallo Kissa052,
deine Aussagen bezüglich den Winkel und Seiten der Dreiecke ist richtig ;)
Du hast nur das Teilmengenzeichen falsch herum gesetzt.(sprich: Menge
ist eine (echte) Teilmenge von Menge
, also es gibt weniger gleichseitige, als gleichschenklige Dreiecke, jedoch ist jedes gleichseitige Dreieck auch gleichschenklig, aber nicht umgekehrt) sowie
. Deine Aussage
stimmt. Setzen wir alles Zusammen erhalten wir:
.
--Tutor: Alex (Diskussion) 17:34, 31. Mai 2017 (CEST)
