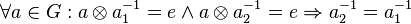Gruppendefinition (kurz): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (→Satz 2) |
*m.g.* (Diskussion | Beiträge) (→Linkseins = Rechtseins) |
||
| Zeile 25: | Zeile 25: | ||
Mit Gleichung (VI) haben wir gezeigt, dass das Linksinverse von <math>a</math> auch Rechtsinverses von <math>a</math> ist. | Mit Gleichung (VI) haben wir gezeigt, dass das Linksinverse von <math>a</math> auch Rechtsinverses von <math>a</math> ist. | ||
| − | =Linkseins | + | =Linkseins gleich Rechtseins= |
==Satz 2== | ==Satz 2== | ||
Es sei <math>[G, \otimes]</math> eine Gruppe. <math>\forall a \in G: a \otimes a_1^{-1} = e \land a \otimes a_2^{-1} = e \Rightarrow a_2^{-1}= a_1^{-1}</math> | Es sei <math>[G, \otimes]</math> eine Gruppe. <math>\forall a \in G: a \otimes a_1^{-1} = e \land a \otimes a_2^{-1} = e \Rightarrow a_2^{-1}= a_1^{-1}</math> | ||
Version vom 25. November 2017, 11:56 Uhr
Linksinvers gleich RechtsinversSatz 1Es sei Beweis von Satz 1Es sei
Mit Gleichung (VI) haben wir gezeigt, dass das Linksinverse von Linkseins gleich RechtseinsSatz 2Es sei |
![[G, \odot]](/images/math/7/3/5/73557169bfbd888213d4a53d2c3ff1e4.png) eine Gruppe.
eine Gruppe.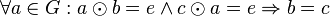
 das Linksinverse bzgl.
das Linksinverse bzgl.  von
von  .
. 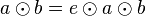
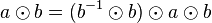
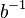

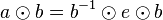
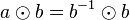
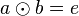
![[G, \otimes]](/images/math/0/1/3/01322720752789c5d9651172aee2d990.png) eine Gruppe.
eine Gruppe.