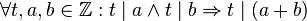Serie 2 SoSe 2018: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „<div style="margin:0; margin-right:4px; border:1px solid #27408B; padding: 1em 1em 1em 1em; background-color:#FFFF99; align:left;"> <!--- Was hier drüber steh…“) |
*m.g.* (Diskussion | Beiträge) |
||
| Zeile 15: | Zeile 15: | ||
d) Beweisen Sie Satz S. | d) Beweisen Sie Satz S. | ||
| − | =Aufgabe 2.1 SoSe 2018= | + | =Aufgabe 2.2 SoSe 2018= |
| + | a) Bilden Sie sie Umkehrung von Satz S aus Aufgabe 2.1.<br /> | ||
| + | b) Begründen Sie: Die Umkehrung von Satz S ist keine wahre Aussage.<br /> | ||
| + | c) Formulieren Sie die Kontraposition von Satz S. | ||
| + | |||
| + | =Aufgabe 2.3 SoSe 2018= | ||
| + | Formulieren Sie den Basiswinkelsatz für Dreiecke in ''Wenn-Dann-Form''. | ||
Version vom 28. April 2018, 10:02 Uhr
Übungsaufgaben zum 04.05.2018
Implikation, Voraussetzung, Behauptung, Umkehrung, Kontraposition, Widerspruchsbeweis, hinreichend, notwendig, hinreichend und notwendig
Aufgabe 2.1 SoSe 2018
Ein Blick über den Tellerrand der Geometrie:
Satz S:
a) Formulieren Sie Satz S schultauglich, d.h. weniger formal in einem normalen deutschen Satz.
b) Wie lautet die Voraussetzung in Satz S?
c) Wie lautet die Behauptung von Satz S.
d) Beweisen Sie Satz S.
Aufgabe 2.2 SoSe 2018
a) Bilden Sie sie Umkehrung von Satz S aus Aufgabe 2.1.
b) Begründen Sie: Die Umkehrung von Satz S ist keine wahre Aussage.
c) Formulieren Sie die Kontraposition von Satz S.
Aufgabe 2.3 SoSe 2018
Formulieren Sie den Basiswinkelsatz für Dreiecke in Wenn-Dann-Form.