Übungsaufgaben zur Algebra, Serie 2 SoSe 2018: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) |
*m.g.* (Diskussion | Beiträge) |
||
| Zeile 3: | Zeile 3: | ||
| valign="top" | | | valign="top" | | ||
=Aufgabe 2.1= | =Aufgabe 2.1= | ||
| − | Gegeben sei <math> | + | Gegeben sei <math>DD_\Delta:=\left [ \left \{ \begin{pmatrix} 1 & 0 \\ 0 & 1 \\ \end{pmatrix}, \begin{pmatrix} -\frac{1}{2} & -\frac{1}{2} \\ \frac{1}{2} \sqrt{3} & -\frac{1}{2} \sqrt{3} \\ \end{pmatrix}, \begin{pmatrix} a & b \\ c & d \end{pmatrix} \right \}, \circ \right ]</math>. <br /> |
| + | Bestimmen Sie <math>a, b, c, d \in \mathbb{R}</math> derart, dass <math>DD_\Delta</math> eine Gruppe ist. Die Operation <math>\circ</math> ist dabei als die normale Matrizenmultiplikation zu verstehen. | ||
| + | =Aufgabe 2.2= | ||
<!--- Was hier drunter steht muss stehen bleiben ---> | <!--- Was hier drunter steht muss stehen bleiben ---> | ||
Version vom 1. Mai 2018, 14:39 Uhr
Aufgabe 2.1Gegeben sei Aufgabe 2.2 |
![DD_\Delta:=\left [ \left \{ \begin{pmatrix} 1 & 0 \\ 0 & 1 \\ \end{pmatrix}, \begin{pmatrix} -\frac{1}{2} & -\frac{1}{2} \\ \frac{1}{2} \sqrt{3} & -\frac{1}{2} \sqrt{3} \\ \end{pmatrix}, \begin{pmatrix} a & b \\ c & d \end{pmatrix} \right \}, \circ \right ]](/images/math/5/f/2/5f20e500bcab3995ec3dca6e5a97b976.png)
. 
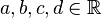derart, dass 
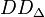eine Gruppe ist. Die Operation 
ist dabei als die normale Matrizenmultiplikation zu verstehen.
