Übungsaufgaben zur Algebra, Serie 3 SoSe 2018: Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(→‎Aufgabe 3.2)
(→‎Aufgabe 3.3)
Zeile 12: Zeile 12:
  
 
=Aufgabe 3.3=
 
=Aufgabe 3.3=
 +
Die Relation quotientengleich <math>=_Q</math> ist eine Äquivalenzrelation auf der Menge aller Brüche und zieht damit eine Klasseneinteilung nach sich. Die Menge aller Äquivalenzklassen nach <math>=_Q</math> ist die Menge der gebrochenen Zahlen <math>\mathbb{Q}^+</math>. Eine gebrochene Zahl <math>\overline{\frac{a}{b}}</math> ist damit eine Äquivalenzklasse nach der Relation <math>=_Q</math>, d.h. der Bruch <math>\frac{e}{f}</math> gehört genau dann zu <math>\overline{\frac{a}{b}}</math>, wenn <math>\frac{e}{f}=_Q\frac{a}{b}</math> gilt. Beweisen Sie die Repräsentantenunabhängigkeit der Multiplikation gebrochener Zahlen.
 +
 
=Aufgabe 3.4=
 
=Aufgabe 3.4=
 
=Aufgabe 3.5=
 
=Aufgabe 3.5=

Version vom 5. Mai 2018, 15:05 Uhr

Inhaltsverzeichnis

Aufgabe 3.1

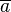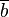Es seien \overline{a} und \overline{b} zwei Restklassen bzgl. des selben Moduls n. Beweisen Sie die Repräsentantenunabhängigkeit Restklassenaddition: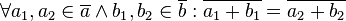
\forall a_1, a_2 \in \overline{a} \land b_1, b_2 \in \overline{b}: \overline{a_1+b_1}=\overline{a_2+b_2}.

Aufgabe 3.2

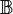Auf der Menge aller Brüche \mathbb{B}definieren wir deine Relation Quotientengleich =_Q:
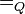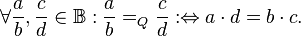
\forall \frac{a}{b}, \frac{c}{d} \in \mathbb{B}: \frac{a}{b} =_Q \frac{c}{d} :\Leftrightarrow a \cdot d = b \cdot c.
Zeigen Sie, dass =_Q eine Äquivalenzrelation ist.

Aufgabe 3.3

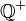Die Relation quotientengleich =_Q ist eine Äquivalenzrelation auf der Menge aller Brüche und zieht damit eine Klasseneinteilung nach sich. Die Menge aller Äquivalenzklassen nach =_Q ist die Menge der gebrochenen Zahlen \mathbb{Q}^+. Eine gebrochene Zahl 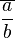\overline{\frac{a}{b}} ist damit eine Äquivalenzklasse nach der Relation 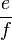=_Q, d.h. der Bruch \frac{e}{f} gehört genau dann zu 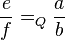\overline{\frac{a}{b}}, wenn \frac{e}{f}=_Q\frac{a}{b} gilt. Beweisen Sie die Repräsentantenunabhängigkeit der Multiplikation gebrochener Zahlen.

Aufgabe 3.4

Aufgabe 3.5

Aufgabe 3.6

Aufgabe 3.7

Aufgabe 3.8

Aufgabe 3.9

Aufgabe 3.10

Von „http://geometrie.zum.de/index.php?title=Übungsaufgaben_zur_Algebra,_Serie_3_SoSe_2018&oldid=31321“