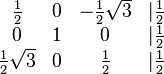Serie 3: LGS lösen SoSe 2018: Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(Die Seite wurde neu angelegt: „<div style="margin:0; margin-right:4px; border:1px solid #27408B; padding: 1em 1em 1em 1em; background-color:#B9D0F0; align:left;"> {|width=90%| style="backgro…“)
 
Zeile 7: Zeile 7:
 
Lösen Sie das folgende Gleichungssystem:<br />
 
Lösen Sie das folgende Gleichungssystem:<br />
 
<math>\begin{pmatrix} \frac{1}{2}\sqrt{2} & - \frac{1}{2}\sqrt{2} \\ \frac{1}{2}\sqrt{2} & \frac{1}{2}\sqrt{2} \end{pmatrix}  \cdot \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 0 \\ 1 \end{pmatrix} </math>.
 
<math>\begin{pmatrix} \frac{1}{2}\sqrt{2} & - \frac{1}{2}\sqrt{2} \\ \frac{1}{2}\sqrt{2} & \frac{1}{2}\sqrt{2} \end{pmatrix}  \cdot \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 0 \\ 1 \end{pmatrix} </math>.
 +
 +
=Aufgabe 3.2 SoSe 2018=
 +
Lösen Sie das folgende Gleichungssystem:<br />
 +
<math>\begin{pmatrix} \frac{1}{2}\sqrt{3} & - \frac{1}{2} \\ \frac{1}{2} & \frac{1}{2}\sqrt{3} \end{pmatrix}  \cdot \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 0 \\ 1 \end{pmatrix} </math>.
 +
 +
=Aufgabe 3.3=
 +
Gegeben ist die große Koeffizientenmatrix eines lineraren Gleichungssystems:<br />
 +
<math>\begin{matrix} \frac{1}{2} & 0 & -\frac{1}{2}\sqrt{3} & \vert \frac{1}{2} \\ 0 & 1 & 0 & \vert \frac{1}{2} \\ \frac{1}{2}\sqrt{3} & 0 & \frac{1}{2} & \vert \frac{1}{2} \end{matrix} </math><br />
 +
Lösen Sie dieses Gleichungssystem.
 +
=Aufgabe 3.4=
 +
 
<!--- hier drunter nichts eintragen --->
 
<!--- hier drunter nichts eintragen --->
 
[[Kategorie:Linalg]]
 
[[Kategorie:Linalg]]

Version vom 6. Mai 2018, 12:13 Uhr

Inhaltsverzeichnis

Aufgabe 3.1 SoSe 2018

Lösen Sie das folgende Gleichungssystem:
\begin{pmatrix} \frac{1}{2}\sqrt{2} & - \frac{1}{2}\sqrt{2} \\ \frac{1}{2}\sqrt{2} & \frac{1}{2}\sqrt{2} \end{pmatrix} \cdot \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 0 \\ 1 \end{pmatrix} .

Aufgabe 3.2 SoSe 2018

Lösen Sie das folgende Gleichungssystem:
\begin{pmatrix} \frac{1}{2}\sqrt{3} & - \frac{1}{2} \\ \frac{1}{2} & \frac{1}{2}\sqrt{3} \end{pmatrix} \cdot \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 0 \\ 1 \end{pmatrix} .

Aufgabe 3.3

Gegeben ist die große Koeffizientenmatrix eines lineraren Gleichungssystems:
\begin{matrix} \frac{1}{2} & 0 & -\frac{1}{2}\sqrt{3} & \vert \frac{1}{2} \\ 0 & 1 & 0 & \vert \frac{1}{2} \\ \frac{1}{2}\sqrt{3} & 0 & \frac{1}{2} & \vert \frac{1}{2} \end{matrix}
Lösen Sie dieses Gleichungssystem.

Aufgabe 3.4

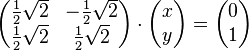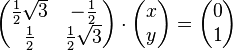Von „http://geometrie.zum.de/index.php?title=Serie_3:_LGS_lösen_SoSe_2018&oldid=31337“