Allgemeine lineare Gleichung mit drei Variablen: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (→Spezialfall: einer der drei Koeffizienten a, b, c ist gleich 0) |
*m.g.* (Diskussion | Beiträge) |
||
| Zeile 37: | Zeile 37: | ||
Die Lösungsmenge unserer Ausgangsgleichung <math>2x+\frac{3}{5}y+0z=1</math> ist damit eine Ebene, die senkrecht auf der | Die Lösungsmenge unserer Ausgangsgleichung <math>2x+\frac{3}{5}y+0z=1</math> ist damit eine Ebene, die senkrecht auf der | ||
<math>x-y-</math>Ebene steht und mit der <math>x-y-</math>Ebene die Gerade <math>y=-\frac{10}{3}x+\frac{5}{3}</math> gemeinsam hat. | <math>x-y-</math>Ebene steht und mit der <math>x-y-</math>Ebene die Gerade <math>y=-\frac{10}{3}x+\frac{5}{3}</math> gemeinsam hat. | ||
| + | ====Allgemeiner Fall: jeder der Koeffizienten a, b, c ist verschieden von 0 ==== | ||
====Ebene!==== | ====Ebene!==== | ||
Version vom 9. Mai 2018, 12:59 Uhr
Allgemeine lineare Gleichung ax + by + cz = d
Grafische Veranschaulichung der Lösungsmenge einer Gleichung vom Typ ax+by+cz=dGerade?Es seien Spezialfall: zwei der Koeffizieneten, a, b, c sind gleich 0Sei etwa nur der Koeffizient
Spezialfall: einer der drei Koeffizienten a, b, c ist gleich 0Beispiel 1Unsere Gleichung lautet für dieses Beispiel Allgemeiner Fall: jeder der Koeffizienten a, b, c ist verschieden von 0Ebene!Satz:
|
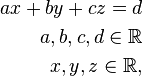
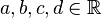 , beliebig aber fest,
, beliebig aber fest, 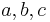 nicht gleichzeitig
nicht gleichzeitig 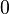 ,
,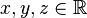 , variabel.
, variabel.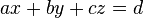
 ließ sich die Koordinaten der Punkte einer Geraden im
ließ sich die Koordinaten der Punkte einer Geraden im 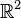 interpretieren.
Man mag schnell geneigt sein, die Lösungsmenge der Gleichung
interpretieren.
Man mag schnell geneigt sein, die Lösungsmenge der Gleichung 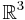 zu interpretieren. Dem ist aber nicht so:
zu interpretieren. Dem ist aber nicht so: verschieden von
verschieden von 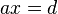 . Umgestellt nach
. Umgestellt nach 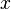 ergibt sich
ergibt sich 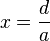 . Alle geordneten Tripel
. Alle geordneten Tripel 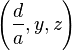 aus dem
aus dem 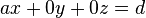 bzw.
bzw. 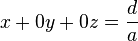 schreiben.
schreiben. interpretieren, die parallel zu einer der Koordinatenebene ist:
interpretieren, die parallel zu einer der Koordinatenebene ist:
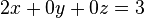 sind die Koordinatentripel aller Punkte der Ebene, die parallel zur
sind die Koordinatentripel aller Punkte der Ebene, die parallel zur 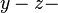 Ebene ist und durch den Punkt mit den Koordinaten
Ebene ist und durch den Punkt mit den Koordinaten  geht.
geht.
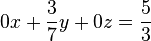 sind die Koordinatentripel aller Punkte der Ebene, die parallel zur
sind die Koordinatentripel aller Punkte der Ebene, die parallel zur 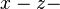 Ebene ist und durch den Punkt mit den Koordinaten
Ebene ist und durch den Punkt mit den Koordinaten 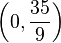 geht.
geht.
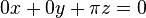 ist die
ist die 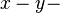 Ebene.
Ebene.
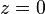
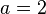
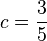
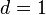
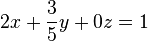
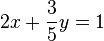 Die Lösungsmenge dieser vereinfachten Gleichung ist eine Gerade in der
Die Lösungsmenge dieser vereinfachten Gleichung ist eine Gerade in der 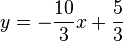 .
. 
