Übungsaufgaben zur Algebra, Serie 5 SoSe 2018: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (→Aufgabe 5.5) |
*m.g.* (Diskussion | Beiträge) (→Aufgabe 5.6) |
||
| Zeile 21: | Zeile 21: | ||
=Aufgabe 5.6= | =Aufgabe 5.6= | ||
| − | + | Bestimmen Sie die zu <math>\begin{pmatrix} 2 & 3 \\ 1 & 4 \end{pmatrix} </math> inverse Matrix. | |
=Aufgabe 5.7= | =Aufgabe 5.7= | ||
Version vom 3. Juni 2018, 14:58 Uhr
Aufgabe 5.1Es sei Aufgabe 5.2Es sei Aufgabe 5.3Beweisen Sie das Untergruppenkriterium 1. Aufgabe 5.4Beweisen Sie das Untergruppenkriterium 2. Aufgabe 5.5Bestimmen Sie die zu Aufgabe 5.6Bestimmen Sie die zu Aufgabe 5.7Aufgabe 5.8Aufgabe 5.9Aufgabe 5.10 |
![[G, \circ]](/images/math/4/6/8/4686bbf90bf7ebab892b288a31255920.png) eine Gruppe mit dem Einselement
eine Gruppe mit dem Einselement  . Beweisen Sie:
. Beweisen Sie: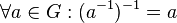 .
.
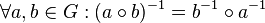 .
.
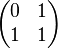 inverse Matrix.
inverse Matrix.
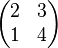 inverse Matrix.
inverse Matrix.

