SoSe 2018 Lösung von Aufgabe 6.01: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(Die Seite wurde neu angelegt: „ Behauptung: Def V <=> Def Ü zz. P Element von AB, d.h. P muss zwischen den Punkten A und B liegen Strecke AB ist größer als Strecke AP“) |
*m.g.* (Diskussion | Beiträge) |
||
| Zeile 1: | Zeile 1: | ||
| − | + | =Aufgabe 6.01 = | |
| + | In einer Übung definierte eine Kommilitonin den Begriff Halbgerade <math>AB^+</math> wie folgt:<br\> | ||
| + | <math>AB^+:=\overline{AB}\cup\left\{P|P\in AB \wedge |AP|> |BP|\right\}</math><br\> | ||
| + | In der Vorlesung wurde wie folgt definiert:<br\> | ||
| + | <math>AB^+:=\overline{AB} \cup \left\{P|\operatorname{Zw}(A,B,P)\right\}</math> | ||
| + | Beweisen Sie: | ||
| + | # Definition V <math>\Rightarrow</math> Definition Ü | ||
| + | # Definition Ü <math>\Rightarrow</math> Definition V | ||
| + | =Lösung 1= | ||
Behauptung: Def V <=> Def Ü | Behauptung: Def V <=> Def Ü | ||
zz. P Element von AB, d.h. P muss zwischen den Punkten A und B liegen | zz. P Element von AB, d.h. P muss zwischen den Punkten A und B liegen | ||
Strecke AB ist größer als Strecke AP | Strecke AB ist größer als Strecke AP | ||
Version vom 10. Juni 2018, 15:27 Uhr
Aufgabe 6.01
In einer Übung definierte eine Kommilitonin den Begriff Halbgerade 
wie folgt:
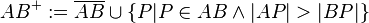
In der Vorlesung wurde wie folgt definiert:
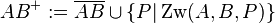Beweisen Sie:
- Definition V
Definition Ü
- Definition Ü Definition V
Lösung 1
Behauptung: Def V <=> Def Ü
zz. P Element von AB, d.h. P muss zwischen den Punkten A und B liegen Strecke AB ist größer als Strecke AP
