Lösung von Zusatzaufgabe 4.2P (WS 18 19): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
| Zeile 3: | Zeile 3: | ||
Der Winkel <math>\alpha</math> wird im Scheitelpunkt durch einen Strahl g geteilt. Es entstehen aus <math>\alpha</math> zwei neue Winkel <math>\beta</math> und <math>\gamma</math> . Wenn <math> | </math> <math>\beta</math> <math> | </math> = <math> | </math> <math>\gamma</math> <math> | </math> , dann ist g die Winkelhalbierende.--Pippilotta Viktualia Rollgardina Pfefferminz Efraimstochter Langstrumpf 22:20, 5. Nov. 2018 (CET) | Der Winkel <math>\alpha</math> wird im Scheitelpunkt durch einen Strahl g geteilt. Es entstehen aus <math>\alpha</math> zwei neue Winkel <math>\beta</math> und <math>\gamma</math> . Wenn <math> | </math> <math>\beta</math> <math> | </math> = <math> | </math> <math>\gamma</math> <math> | </math> , dann ist g die Winkelhalbierende.--Pippilotta Viktualia Rollgardina Pfefferminz Efraimstochter Langstrumpf 22:20, 5. Nov. 2018 (CET) | ||
| + | |||
| + | aber wie konstruiere ich das?--[[Benutzer:Schnirch|Schnirch]] ([[Benutzer Diskussion:Schnirch|Diskussion]]) 13:29, 7. Nov. 2018 (CET) | ||
[[Category:Geo_P]] | [[Category:Geo_P]] | ||
Version vom 7. November 2018, 13:29 Uhr
Geben Sie eine genetische Definition des Begriffs Winkelhalbierende an.
Der Winkel 
wird im Scheitelpunkt durch einen Strahl g geteilt. Es entstehen aus zwei neue Winkel 
und 
. Wenn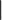 
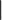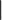
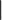= , dann ist g die Winkelhalbierende.--Pippilotta Viktualia Rollgardina Pfefferminz Efraimstochter Langstrumpf 22:20, 5. Nov. 2018 (CET)
aber wie konstruiere ich das?--Schnirch (Diskussion) 13:29, 7. Nov. 2018 (CET)
