Lösung von Zusatzaufgabe 4.2P (WS 18 19): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
CIG UA (Diskussion | Beiträge) |
|||
| Zeile 5: | Zeile 5: | ||
aber wie konstruiere ich das?--[[Benutzer:Schnirch|Schnirch]] ([[Benutzer Diskussion:Schnirch|Diskussion]]) 13:29, 7. Nov. 2018 (CET) | aber wie konstruiere ich das?--[[Benutzer:Schnirch|Schnirch]] ([[Benutzer Diskussion:Schnirch|Diskussion]]) 13:29, 7. Nov. 2018 (CET) | ||
| + | |||
| + | Man zeichne 2 Geraden a und b, die weder parallel, noch identisch sind. Im Punkt A treffen sie im Winkel α aufeinander. Nun konstruiert man eine weitere Gerade c, die a und b in A schneidet und zu beiden Geraden in einem Winkel von |α/2| steht. C ist somit die Winkelhalbierende für α.--[[Benutzer:CIG UA|CIG UA]] ([[Benutzer Diskussion:CIG UA|Diskussion]]) 21:07, 7. Nov. 2018 (CET) | ||
[[Category:Geo_P]] | [[Category:Geo_P]] | ||
Version vom 7. November 2018, 21:07 Uhr
Geben Sie eine genetische Definition des Begriffs Winkelhalbierende an.
Der Winkel 
wird im Scheitelpunkt durch einen Strahl g geteilt. Es entstehen aus zwei neue Winkel 
und 
. Wenn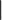 
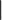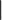
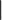= , dann ist g die Winkelhalbierende.--Pippilotta Viktualia Rollgardina Pfefferminz Efraimstochter Langstrumpf 22:20, 5. Nov. 2018 (CET)
aber wie konstruiere ich das?--Schnirch (Diskussion) 13:29, 7. Nov. 2018 (CET)
Man zeichne 2 Geraden a und b, die weder parallel, noch identisch sind. Im Punkt A treffen sie im Winkel α aufeinander. Nun konstruiert man eine weitere Gerade c, die a und b in A schneidet und zu beiden Geraden in einem Winkel von |α/2| steht. C ist somit die Winkelhalbierende für α.--CIG UA (Diskussion) 21:07, 7. Nov. 2018 (CET)
